StepTool: A Step-grained Reinforcement Learning Framework for Tool Learning in LLMs

• Link: https://arxiv.org/pdf/2410.07745
• 깃허브: https://github.com/yuyq18/StepTool

0. Abstract

• 대형 언어 모델 (Large Language Model, LLM)의 강력한 논리 및 추론 능력에도 불구하고 LLM은 여전히 복잡한 문제를 풀기 위해 실시간 정보 검색이나 특정 도메인의 전문 지식을 필요로 함 → 이를 도구 학습 (Tool Learning)이라고 함
• 기존 tool learning 기법들의 한계
  • 주로 전문가의 도구 선택 과정을 언어적 관점에서 토큰 시퀀스를 학습하는 방식으로 튜닝
  • 이 방식은 정적인 선택 과정을 모방하므로 새로운 문제에 대해 일반화하는 능력이 제한됨
  • 또한 전문가의 도구 선택 과정이 최적이 아니고 더 나은 방법이 있을 가능성이 있음
• 이에 따라 본 논문에서는 LLM의 도구 학습을 개선하기 위한 새로운 단계적 (Step-grained) 강화학습 프레임워크 제안 → StepTool
• 해당 기법은 2가지 요소로 구성됨
  • Step-grained Reward Shaping: 도구 호출이 성공했는지, 이것이 얼마나 문제 해결에 기여했는지를 기반으로 각 도구 호출에 대해 보상을 할당
  • Step-grained Optimization: 정책 경사 (Policy Gradient) 방식을 사용하여 다수의 스텝에 대해 모델을 최적화
• 실험 결과는 StepTool이 다수의 스텝, 도구 기반 문제에서 기존 기법의 성능을 능가하는 것을 보임 → 복잡한 문제에 대해 강인한 해결 방법을 제안

1. Introduction

• LLM은 논리와 추론 능력에 있어서 뛰어난 성능을 보이며 다양한 문제에 대해 탁월한 성능을 보임
• 하지만 몇몇 복잡한 문제는 실시간 정보나 도메인 특화 지식을 요구하며 이런 문제는 LLM 자체의 지식만으로는 풀기 어려움
• 이에 따라 최근 외부 도구 (APIs)를 통해 LLM을 강화하는 방법인 도구 학습 (Tool Learning)이 사용됨
• 그림 1과 같이 LLM이 동적으로 도구를 선택하고, 호출하고, 상호작용하며 실시간 응답을 받음

• 외부 도구를 사용한 다수의 상호작용 스텝 이후 LLM은 효과적으로 복잡한 문제를 풀기 위해 필요한 정보들을 수집
• LLM의 도구 학습 능력을 향상 시키기 위한 방법 1 → Supervised Fine Tuning (SFT)
  • LLM이 전문가에 의해 생성된 도구 선택 경로 (trajectory)를 모방하도록 학습
  • 각 경로는 사용자의 쿼리, 다수의 도구 호출과 응답에 대한 시퀀스로 구성 (그림 1 참고)
  • SFT는 LLM을 도구 학습에 사용하기 위해 학습할 때 2가지 한계를 가짐
    • 사전에 정의된 정적인 도구 시퀀스를 모방하므로 새로운 문제나 환경에서 모델이 적응하는 능력을 제한
    • 전문가의 경로는 문제를 성공적으로 해결하지만 도구 호출의 최적 시퀀스는 아닐 수 있음
• LLM의 도구 학습 능력을 향상 시키기 위한 방법 1 → Reinforcement Learning (RL)
  • 도구 학습을 순차적 결정 문제로 설정
  • 각 도구 호출 스텝이 행동 (action)이고 이것이 상태 변환을 일으킴 → 모델은 행동-상태 변환으로 부터 학습
  • 기존의 연구들은 사람의 선호 (RLHF)에 일치하도록 LLM을 최적화하는 학습 방식을 사용
  • 하지만 이런 방법은 몇가지 이유로 도구 학습에 적절하지 않음
    • 도구 학습은 다수의 결정 단계와 실시간 피드백을 포함 → 하지만 RLHF는 단일 스텝을 기반으로 하고 환경으로부터의 피드백이 없음
    • 도구 학습의 각 단계의 보상은 더욱 복잡함 → 도구 호출 성공 뿐 아니라 이것이 문제 해결에 얼마나 기여했는지도 고려해야함
• 본 논문은 도구 학습을 위한 새로운 단계적 강화학습 프레임워크인 StepTool을 제안
  • 도구 학습을 순차적 결정 과정으로 모델링하고 각 도구 상호작용을 문제 해결에 직접 영향을 미치는 결정 지점으로 취급
  • 그림 1과 같이 StepTool은 2가지 주요 요소로 구성됨
    • Step-grained Reward Shaping
      • 각 스텝마다 도구 호출에 대한 정확도와 전체적인 문제 해결에 대한 기여도를 보상으로 디자인
    • Step-grained Optimization
      • 단계적 강화학습 기반 최적화 방법에 기반한 정책 경사 이론을 제안
  • 본 논문의 기법은 동적이고 다수의 스텝에 대해 상호작용을 수행하며, RLHF와 같은 단일 스텝 접근의 한계를 해결
• Contribution
  • 도구 학습에 있어 정적인 SFT 방식의 한계와 기존 RLHF 기반의 방법의 부적절성을 확인
  • 단계적 강화학습 프레임워크인 StepTool 제안 → 도구 학습을 다수의 스텝으로 구성된 의사 결정 과정으로 생각하여 모델이 실시간으로 행동-상태 변환에 대한 환경의 피드백을 받아 학습을 수행
  • 도구 학습 시나리오를 위한 단계적 보상을 디자인 → 도구 호출의 정확도, 전체 문제에 대한 기여를 기반으로 설계
  • 추가적으로 정책 경사를 기반으로하는 단계적 최적화 기법을 제안 → 동적, 다중 스텝 상호작용에 적응하는 것을 보장
  • 3개의 오픈소스 모델들과 비교 실험을 수행하여 StepTool의 효율성을 증명 → 복잡한 문제 해결에 성능을 향상시키는 것을 확인

2. Problem Formulation

• LLM의 도구 학습 과정을 다중 스텝 의사 결정 문제로 모델링 → Markov Decision Process (MDP)로 정의
• MDP는 $M=(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma)$로 나타낼 수 있으며 각 의미는 다음과 같음
  • $\mathcal{S}$: 상태 공간이며 각 상태 $s_t \in \mathcal{S}$는 시간 $t$에서 현재 컨텍스트나 환경 응답을 나타냄
  • $\mathcal{A}$: 행동 공간이며 각 행동 $a_t \in \mathcal{A}$는 시간 $t$에 외부 도구 (API) 호출이나 최종 응답 생성을 생성하는 것
  • $\mathcal{P}$: 상태 변환 확률로 $\mathcal{P}(s_{t+1}|a_t, s_t)$는 상태 $s_t$와 행동 $a_t$가 주어졌을 때 새로운 상태 $s_{t+1}$로 변환할 확률을 나타냄 → 도구의 적용에 따라 어떻게 환경이 변하는지 나타냄
  • $\mathcal{R}$: 보상함수이며 현재 상태 $s_t$, 행동 $a_t$에 기반하여 보상 $r_t = \mathcal{R}(s_t, a_t)$를 할당 → 도구 호출 단계의 효율성을 나타냄
  • $\gamma$: 감가율로 즉각적인 보상과 장기적인 보상에 대한 균형을 결정
• LLM의 도구 선택 전략을 의사 결정 정책 $\pi_{\theta}$로 수식화 (파라미터: $\theta$)
  • $\pi_{\theta}$: 현재 상태가 주어졌을 때 행동 (도구)의 선택을 결정
  • 경로 $\tau \{s_1, a_1, s_2, a_2, ..., s_T, a_T\}$는 시간에 따른 상태와 행동의 시퀀스를 나타냄 → LLM과 외부 도구 혹은 환경 사이의 다중 상호작용을 나타냄
• 최종 문제 해결 성능을 최대화하기 위해 모델은 기대 보상 $\bar{R_{\theta}}$를 최적화
  • $R(\tau)$: 주어진 경로 $\tau$에 대한 보상
  • $\pi_{\theta}(\tau)$: 정책 $\pi_{\theta}$에서 경로를 생성할 확률

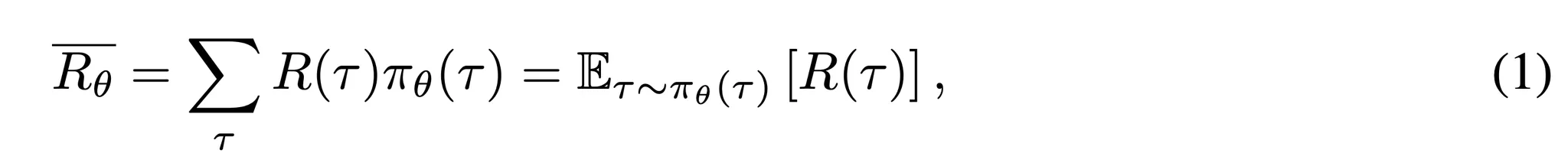
• 기대 보상의 기울기는 모델 파라미터 업데이트에 계산될 수 있음 → LLM의 문제 해결 능력을 향상

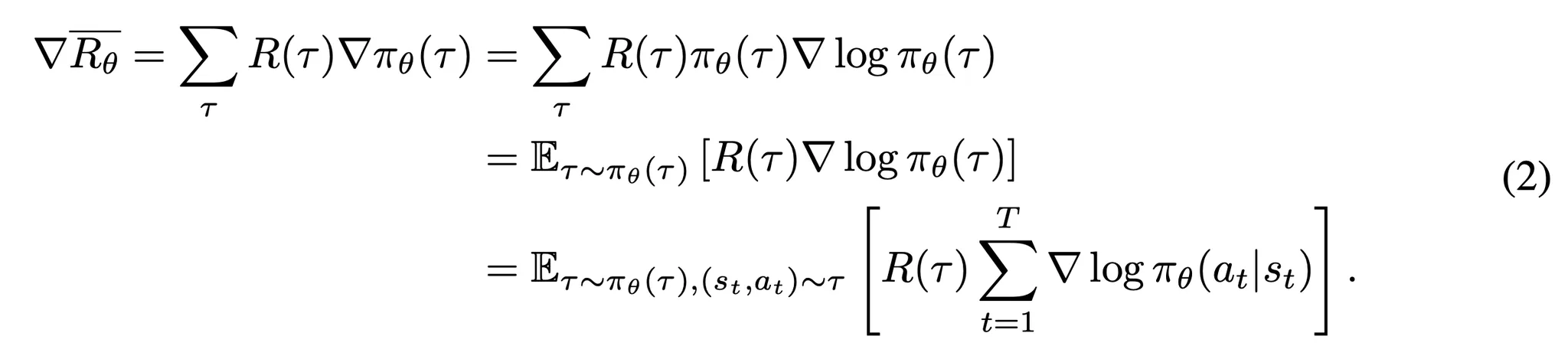
• 대부분의 정책 기울기 기반 강화학습 알고리즘과 같이 학습 효율 향상과 학습 안정화를 위해 R(\tau)를 어드밴티지 함수 \hat{A}(s_t, a_t)로 대체 → 상태의 가치에 대한 행동의 상대 가치를 특정
  • $G_t^n$: 예측된 미래 보상
  • $V(s_t)$: 가치 함수 (현재 정책을 따를 때 상태 $s_t$로부터 시작했을 때 기대되는 반환값을 추정)

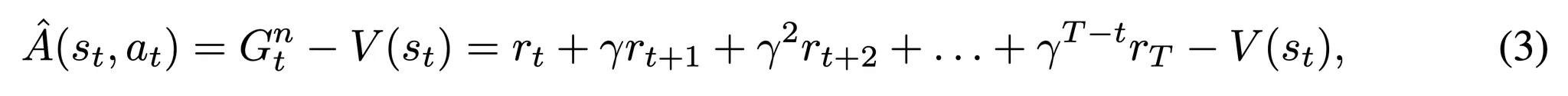
3. Method

• StepTool은 어드밴티지 함수 (식 3)과 정책 경사 수식 (식 2)의 주요 원리에 따라 디자인 됨
• 그림 2와 같이 StepTool은 2가지 주요 요소로 구성되어 있음

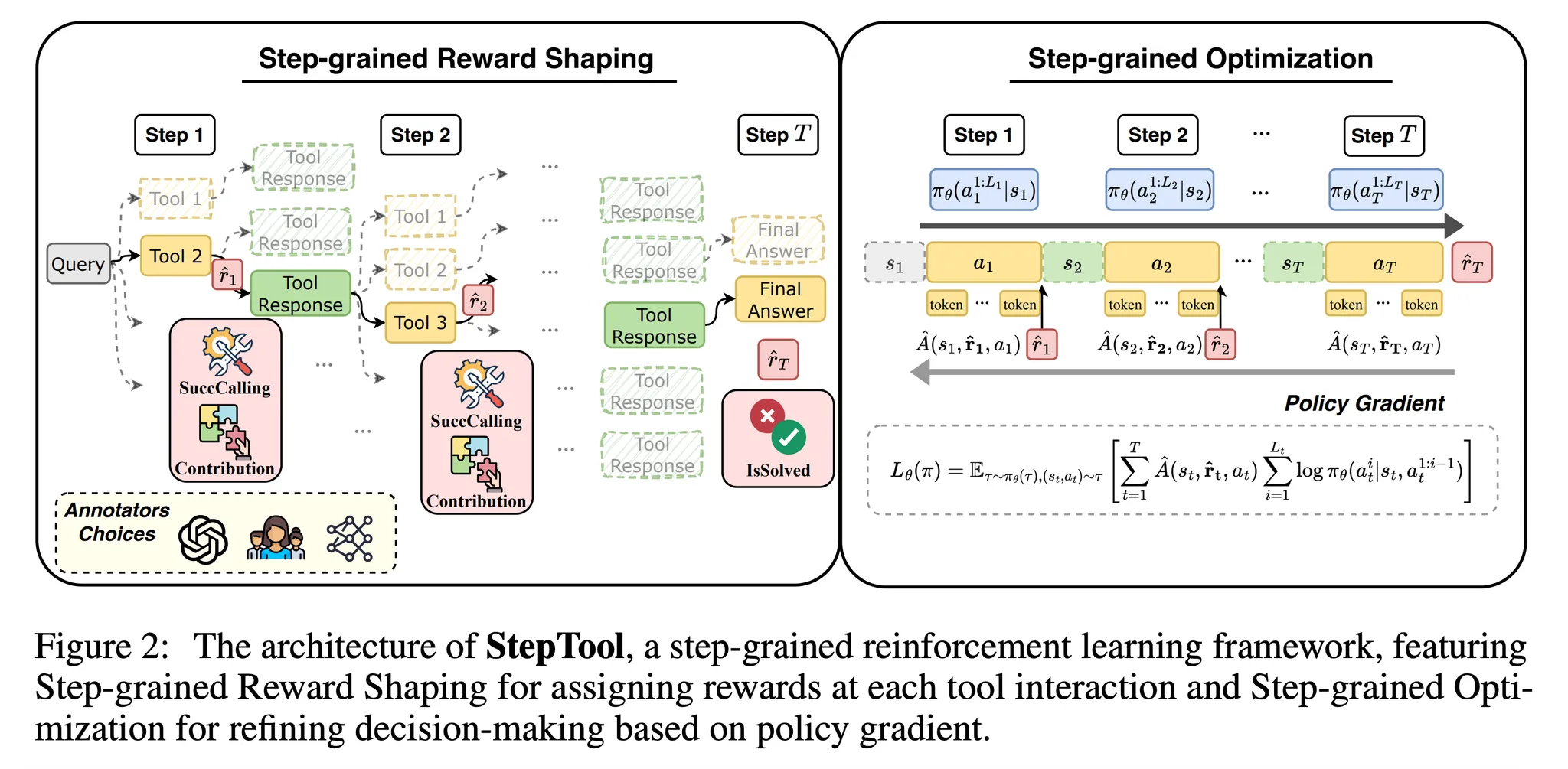
3.1. Step-grained Reward Shaping

• Step-grained Reward Shaping은 중간 과정에서 스텝 단계의 보상을 제공 → 효율적으로 모델이 의사 결정을 하도록 가이드
• 이런 단계적 (step-grained) 보상은 각 행동에 대해 명시적인 피드백을 제공하여 지연된 보상 (delayed reward)의 한계를 극복

3.1.1. Step-grained Reward Design

• 도구 호출 행동의 잘 정의된 형식과 명시적인 문제 목표를 고려하여 2개의 핵심 요소를 디자인
  • 도구 호출 행동의 성공 여부 (SuccCalling)와 문제 해결에 대한 기여 (Contribution)
  • 최종적으로 문제의 달성에 대한 보상을 고려 (IsSolved) → 유저의 쿼리가 풀렸는가를 나타냄

SuccCalling

• SuccCalling 지표는 모델이 정확한 형식과 내용으로 도구 호출을 성공적으로 수행했는지 평가 - i.e. 도구의 이름과 인수 (argument) → $\hat{r}t^{SC} = SuccCalling(a_t, s{t+1})$로 정의
• 하지만 단순히 도구를 잘 호출하는 것은 문제 해결을 보장하지는 않음 → Contribution 지표를 사용하여 도구의 행동이 전체 문제 해결에 얼마나 도움을 주었는지 평가

Contribution

• Contribution 지표는 도구의 행동이 전체적인 문제 해결에 도움이 되었는지를 평가
• 필요 없는 추가 스텝이나 관련 없는 출력과 같이 최소한으로 기여하는 행동을 낮은 보상을 받음
• Contribution 점수는 현재 행동과 최종 문제 해결 행동 사이의 관계에 기반 → $\hat{r}_t^{Con} = Contribution(a_t, a_T)$로 정의

IsSolved

• 최종 단계의 보상은 문제가 성공적으로 해결되었는지와 직접적으로 연관이 있음
• 초기 사용자의 쿼리에 기반한 최종 응답을 평가 → $\hat{r}_t^{IS} = IsSolved(q, a_T)$로 정의
• 보상은 오직 사용자의 쿼리에 대한 최종 단계 응답의 정답 여부에 의존
• 이에 따라 스텝 $t$에서 각 행동의 보상을 다음과 같이 정의할 수 있음
  • \alpha: 각 요소에 대한 가중치

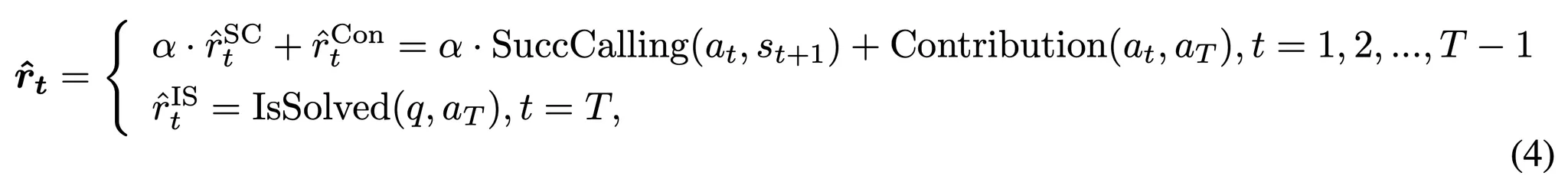
• 중간 단계의 보상과 최종 스텝의 보상은 모두 uniform 스케일로 정규화

3.1.2. Step-grained Reward Acquisition

• 단계적 보상을 포함하는 학습 데이터 생성을 위해 먼저 학습셋 문제에 대한 모델의 추론을 통해 다수의 경로를 취득 → 각 경로는 외부 도구나 환경과 모델 사이에서 일어나는 다수의 상호작용으로 구성되어 있음
• 본 논문에서는 규칙 기반 시스템과 GPT-4를 이용하여 보상을 생성 → 참조 C의 그림 6 참고

• 위와 같은 단계적 데이터는 오프라인 강화학습의 최적화에도 사용될 수 있고 온라인 학습을 위한 보상 모델 학습에도 사용될 수 있음

3.2. Step-grained Optimization

3.2.1. Step-grained Optimization Objective

• 이제 토큰 단위로 기대 보상의 경사 (gradient)를 계산
• 각 행동 $a_t$가 $L_t$ 토큰들의 시퀀스로 구성되어 있을 때, 스텝 단계에서 기대되는 반환값 $\bar{R_{\theta}}$의 경사는 다음과 같음

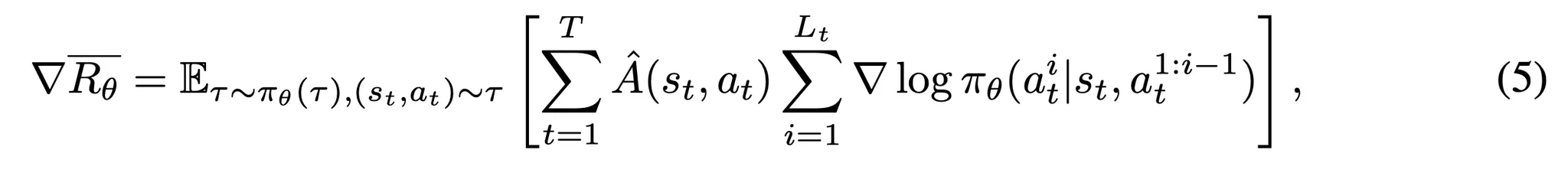
• $\hat{A} (s_t, a_t)$: 스텝 $t$에서 행동 시퀀스 $a_t$ ($L_t$개의 토큰들로 구성)에 대한 어드밴티지를 나타냄
  • 각 행동 시퀀스의 어드밴티지를 . 잘반영하기 위해 단계별 보상 $\hat{r}_t$를 사용해서 어드밴티지 함수 $\hat{A} (s_t, a_t)$를 다음과 같이 구현
    
    • $G_t^n$은 단계별 보상 $r_t$ $r_t$$\gamma$에 의해 감가된 누적 미래 보상을 나타냄
    • $V(s_t)$는 현재 상태의 가치 함수

 

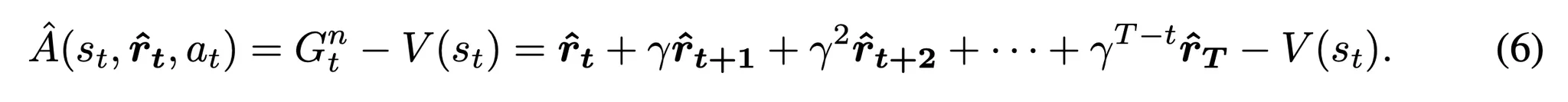
• 최적화 목적함수는 다음과 같이 수식화 → 스텝 단계의 어드밴티지에 따라 정책 \pi_\theta를 최적화하는 목적함수

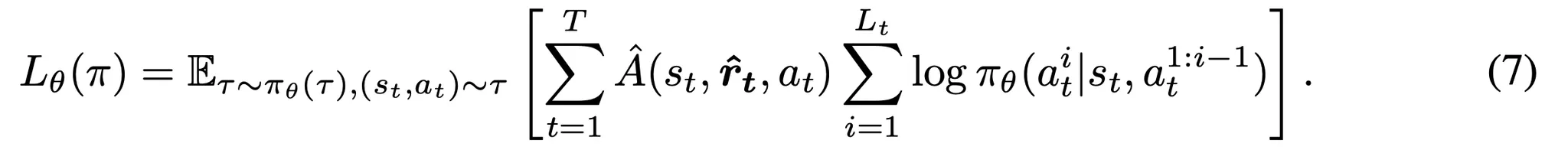
• 추가적으로 이를 기존 RLHF와 비교해보자
  • 해당 기법은 “프롬프트 응답”에 대한 사람의 선호를 기반으로 구한 최종 보상을 최적화 → 문제를 단일 스텝 ( $T=1$)로 고려한 것과 동일
  • 그러나 도구 학습 시나리오는 다수의 스텝에 대한 상호작용을 포함하며 각 경로는 다수의 중간 스텝들로 구성되어 있음
  • 본 논문의 기법은 각 스텝에서 단계별 보상과 최적화를 적용하여 $T>1$의 더욱 복잡한 케이스를 해결

3.2.2. A Practical Instantiation with PPO

• 정책 기반 강화학습 알고리즘 중 PPO (Proximal Policy Optimization) 알고리즘을 사용
• 어드밴티지는 안정성 향상을 위해 GAE (Generalized Advantage Estimation)을 사용하여 추정

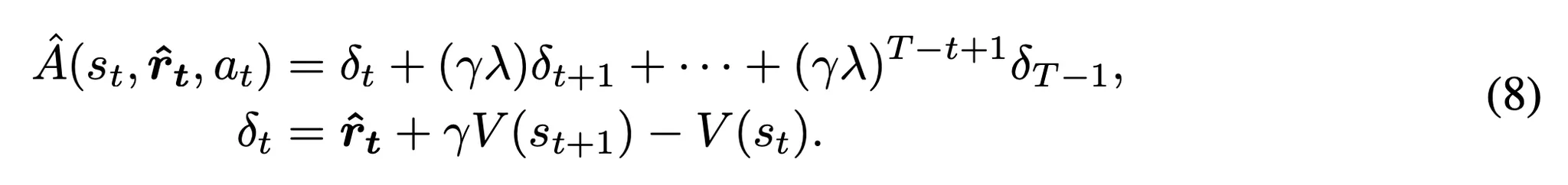
• 안정적인 학습을 위해 PPO-clip 버전을 사용 → 최적화 중 큰 업데이트를 방지
• Clipped PPO의 목적함수
  • $\pi_{\theta'}$: 이전의 경로를 생성한 과거의 정책
  • $\epsilon$: 현재와 과거 정책 사이의 허용가능한 편차를 조절하는 하이퍼파라미터

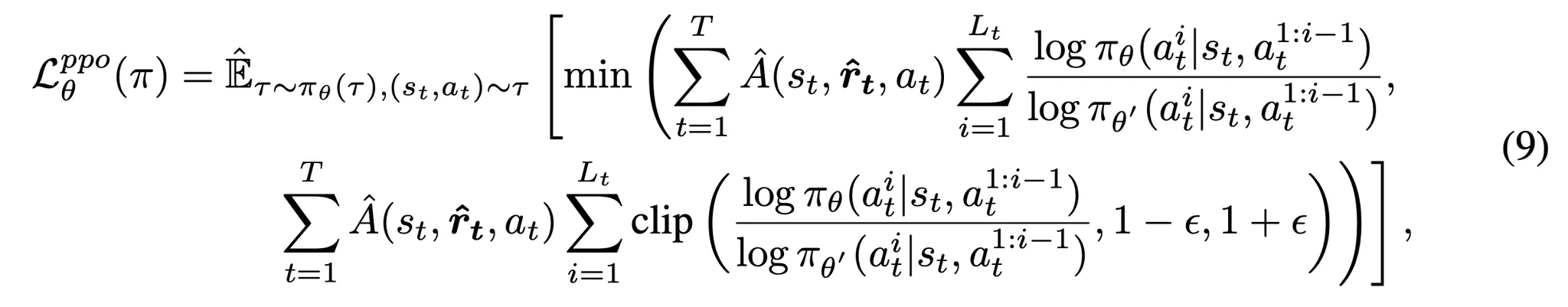
• 안정적 학습을 위해 각 토큰에 대해 과거 정책으로부터 per-token KL divergence penalty를 사용 (RLHF에서 제안된 기법) → 최적화 중 큰 정책 변화를 방지

4. Experiments

4.1. Experimental Settings

Benchmark & Evaluation Metrics

• StableToolBench 사용 → 765개의 문제와 6개의 하위 항목으로 구성되었으며 다양한 도구 카테고리와 복잡성을 제공
• 2개의 주요한 지표를 사용하여 평가
  • pass rate: 모델이 해결한 문제의 비율을 측정
  • win rate: 얼마나 자주 모델이 다른 베이스라인의 성능을 능가했는지 측정
• StableToolBench의 테스트 문제들에 대한 통계는 아래의 표 1 참고

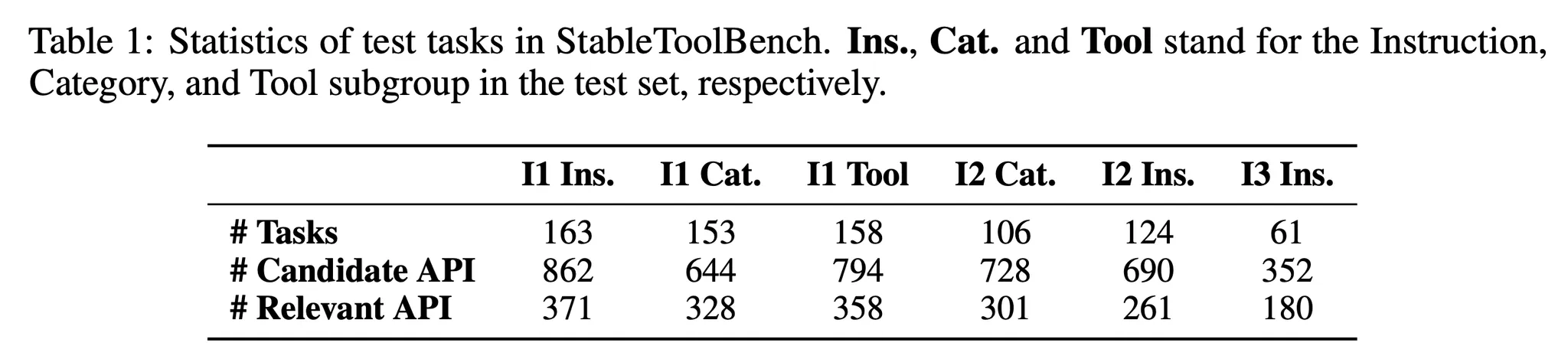
Baselines

• 기존의 도구 학습은 대부분 SFT를 통해 수행 → 동일한 데이터로 학습한 SFT를 베이스라인으로 사용
• 또한 강화학습 기반의 도구 학습으로는 RLHF-PPO를 베이스라인으로 사용
• 3개의 오픈소스 모델을 사용하여 평가
  1. ToolLLaMA-2-7b-v2 (ToolLlama)
  2. Llama3.1-8B-Instruct (Llama3.1)
  3. Qwen2-7B-Instruct (Qwen2)
• 2개의 전략을 사용
  • Chain of Thought (CoT)
  • Depth-First Search Decision Tree (DFSDT)
• 비교 데이터를 구축해야하는 이유로 DPO (Directed Preference Optimization)은 제외

Training Setting

• SFT를 위해 Llama3.1과 Qwen2를 GPT-4로 부터 얻은 정적인 전문가 데이터로 학습 → ToolBench에서 샘플링 한 문제들로 학습
• ToolLlama는 이미 유사하게 사전학습 되었으므로 그대로 사용
• RLHF-PPO와 StepTool에 대해서는 5000개의 학습 문제에서 샘플링 된 사용자 쿼리를 통해 각 모델의 응답과 상호작용 경로를 생성
• 단계별 보상 설정을 위해서 규칙 기반 모델과 GPT-4 (gpt-4-turbo-2024-04-09) 사용
• 학습 파라미터 및 조건
  • 학습률 = $1e^{-5}$, 배치사이즈 = 8, 초기 KL 계수 = 0.3, 4개의 NVIDIA A100 GPU 사용

4.2. Main Results

• 표 2는 3개의 베이스 모델과 2개의 전략을 통해 SFT와 RLHF-PPO, StepTool 사이의 성능을 비교
  • gpt-3.5-turbo-0125는 참조용 벤치마크로 사용

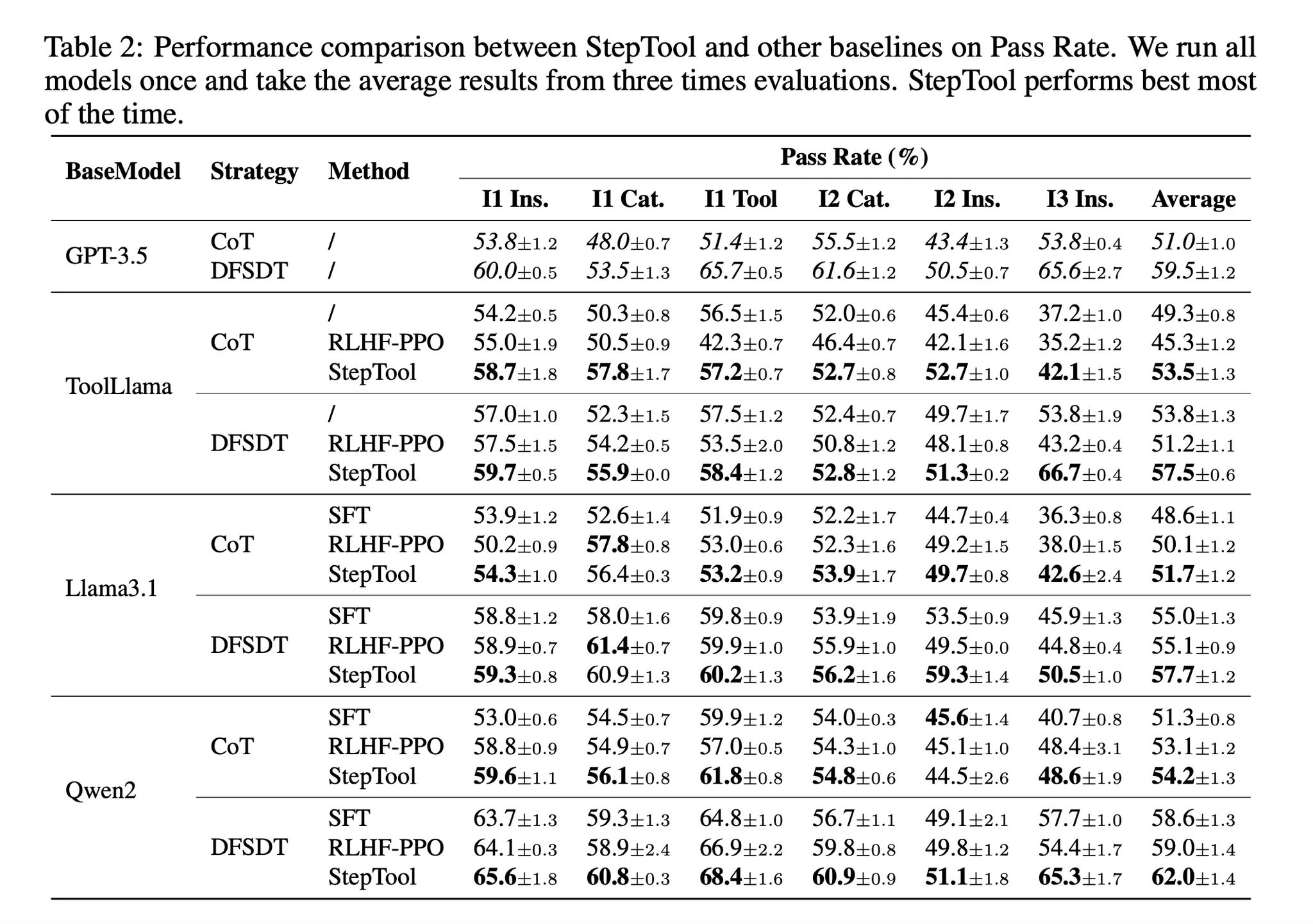
• StepTool이 일관적으로 SFT와 RLHF-PPO의 성능을 대부분의 하위 문제에서 능가 → 특히 Qwen2로 DFSDT 전략을 테스트한 경우 StepTool이 ‘I2 Ins’를 제외하고 모든 하위 문제에서 60% 이상의 pass rate을 달성
• 다양한 하위항목에 대해 개선 달성 → 간단한 하위 항목인 I1 Tool 같은 것에 대해서는 StepTool이 1% - 4% 정도의 낮은 성능 향상을 보임, 하지만 ‘I3 Ins’와 같은 복잡한 하위 항목에서는 개선이 5% - 13%로 큼 → 즉, StepTool은 다수의 도구와 카테고리를 가지는 복잡한 문제에서 강점을 가짐
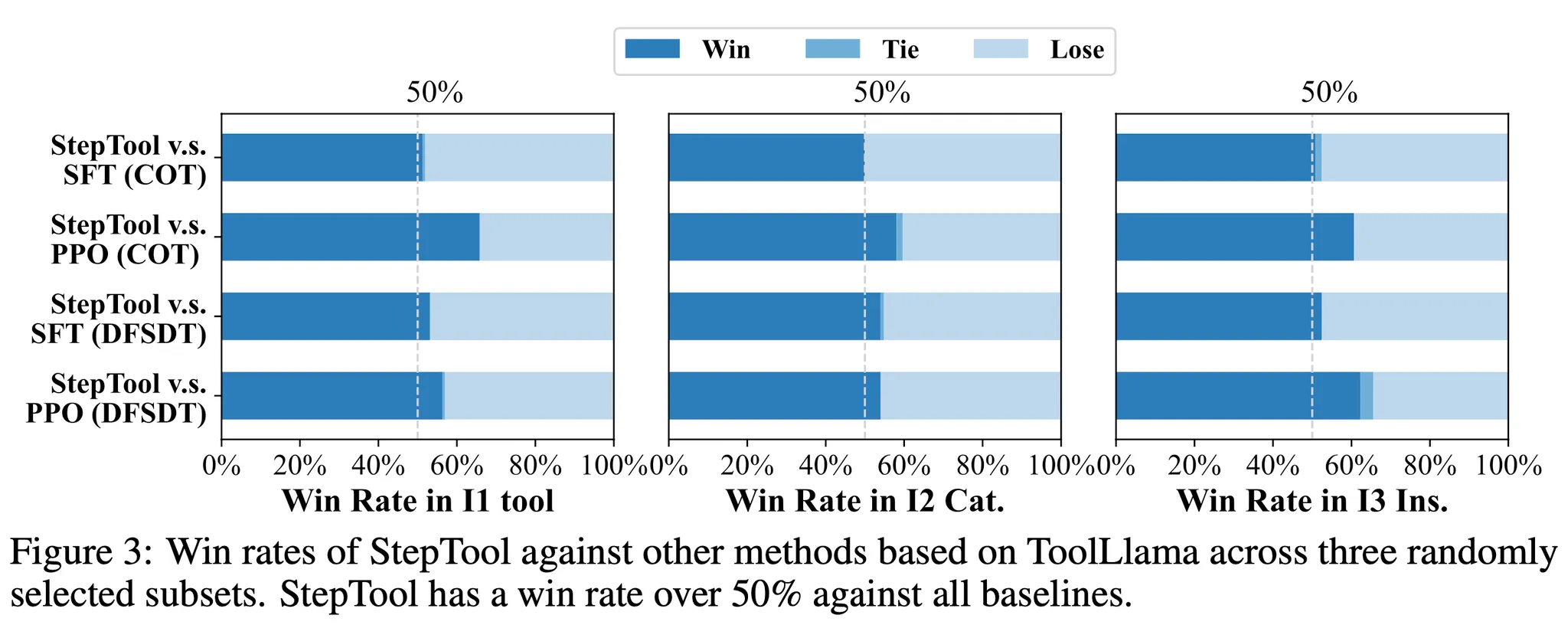
• StepTool은 win rate 지표를 참고했을 때 더 좋은 해결을 위한 경로를 찾는다는 것을 알 수 있음 → 그림 3을 보면 StepTool의 win rate가 3개의 하위 항목에서 베이스라인들에 비해 좋은 성능을 달성 → ToolLLaMA에서 SFT와 RLHF-PPO에 비해 win rate가 50% ~ 65.8%로 더 좋은 성능을 보임

4.3. Pass@k: Assessing Knowledge Discovery vs. Prior Re-weighting

• 수학적 추론과 같은 도메인에서 주로 사용하는 Pass@k 지표 계산 → StepTool이 새로운 지식을 찾거나 사전 지식의 가중치를 재조정 할 수 있다는 것을 보임
• 실험은 CoT 전략에서 ToolLlama에 StepTool 최적화 전과 후 비교 → Temperature 0.7로, 8개의 경로를 샘플링 하여 실험
• 표 3을 보면 StepTool로 최적화 한 ToolLlama가 Pass@2, Pass@4, Pass@8의 대부분의 실험에서 더 뛰어난 성능을 보임

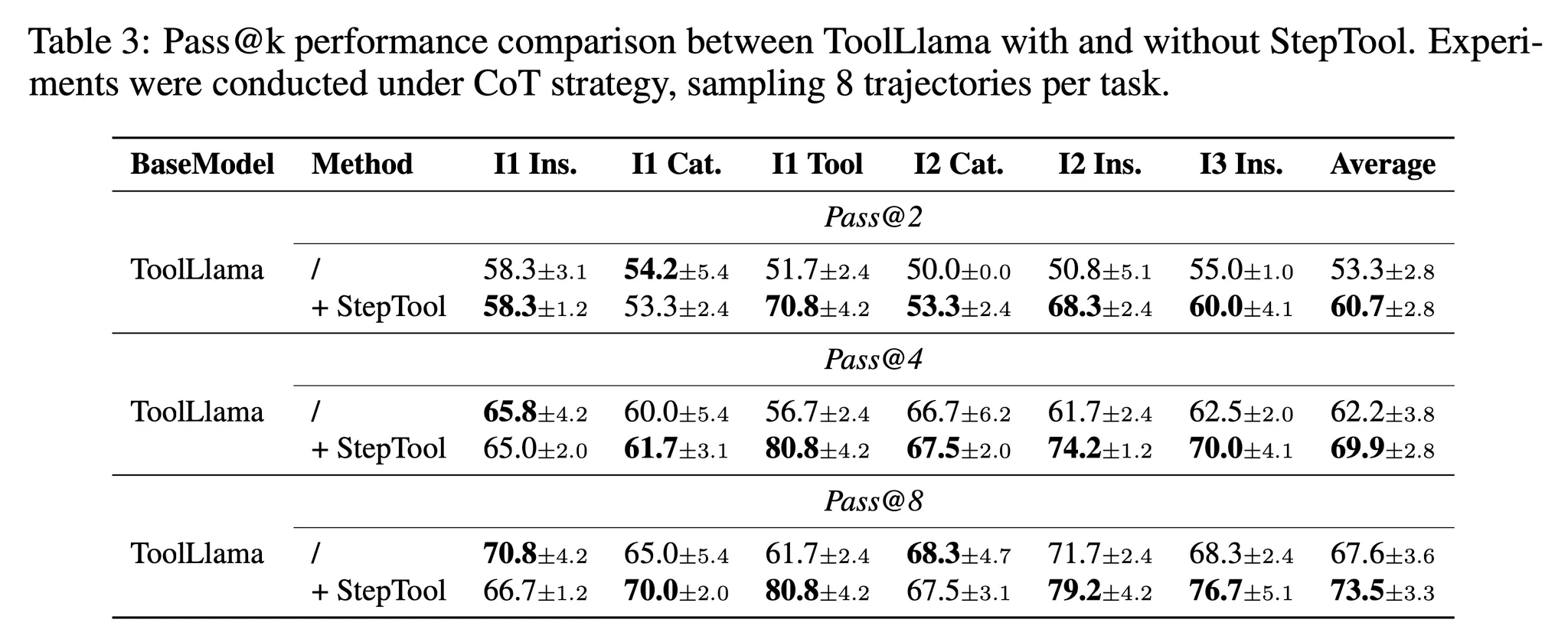
• 개선된 Pass@k 점수는 모델이 강화학습 최적화를 통해 사전 지식에 대한 재조정을 했을 뿐 아니라 새로운 지식을 탐색했다는 것도 알 수 있음

4.4. Ablation Study: Impact of Step-grained Components

• StepTool에서 각 단계별 요소의 기여를 평가하기 위해 2개의 변경 사항에 대한 실험 수행
  • w/o Step-grained Reward → 중간 보상을 0으로 설정
  • w/o Step-grained Opt → 하위 경로가 중간 경로에서 종료되고 PPO로 최적화
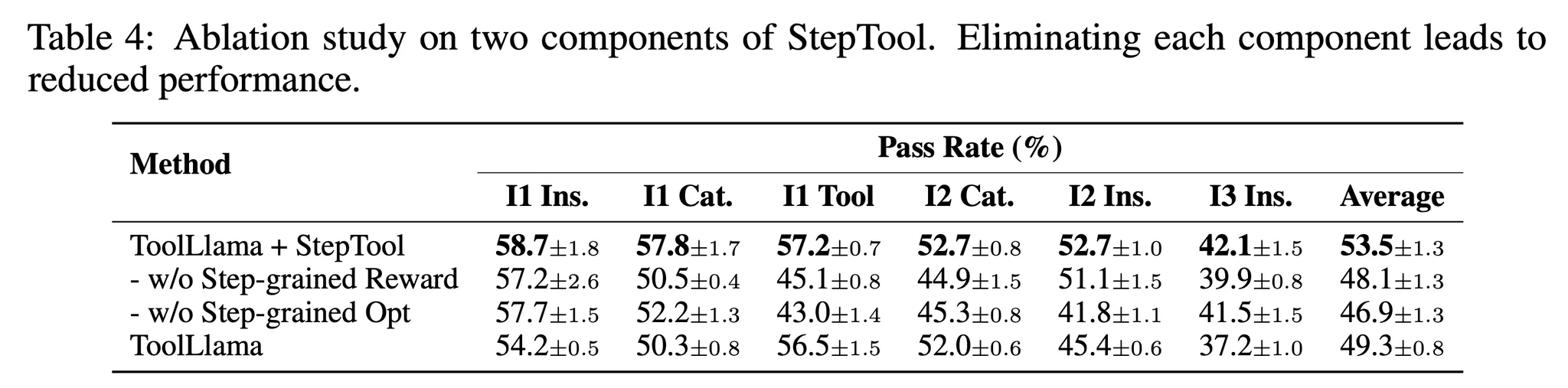
• 표 4를 참고하면 단계별 보상이나 단계별 최적화를 제거하는것이 성능에 큰 하락을 가지고 오는 것을 알 수 있음 → 이 결과를 통해 중간 보상의 중요성이나 RLHF-PPO와 같이 스텝에 대한 의존성에 한계를 확인할 수 있음

4.5. Analysis of Tool Invocation Success Rates

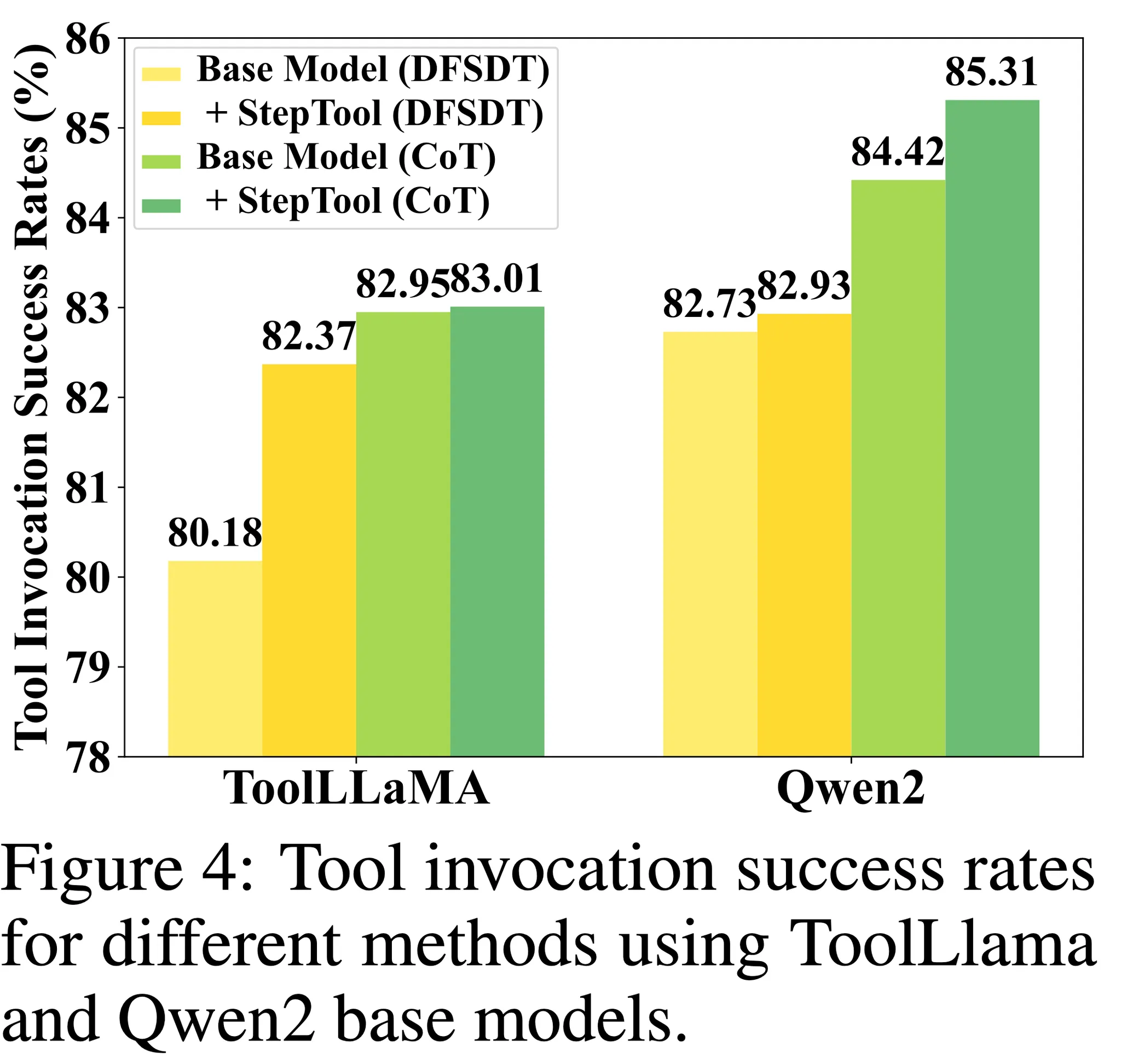
• 중간 단계에서 본 기법을 통해 도구 호출을 개선하는 것의 효율성을 검증하기 위해 ToolLLaMA와 Qwen2 모델 모두 테스트 셋의 중간 단계에서 도구 호출의 평균 성공률을 계산
• 그림 4에서 확인할 수 있는 것 처럼 StepTool이 CoT와 DFSDT 세팅에서 중간 도구 호출의 성공률을 상승시킴 → 다수 단계의 문제에서 도구 정확도와 효율성을 개선

4.6. Qualitative Analysis

• 정성적인 분석을 통해 StepTool이 중간 행동을 어떻게 개선하는지 이해해보자
• 그림 5는 StepTool이 ToolLlama의 잘못된 도구 선택을 개선하는 상황을 보여줌

• 사용자가 채널의 정보, 비디오 댓글, 영화의 스트리밍 출처를 요청
• ToolLlama가 처음에는 정확한 채널과 비디오 댓글을 검색했지만 ‘download_stream’ 도구 대신 ‘getvideoscomment’를 실수로 다시 요청
• 하지만 StepTool 적용 이후에는 모델이 정확하게 ‘download_stream’ 도구를 사용하는 것을 확인할 수 있음 → 스트리밍 링크를 제공하며 요청을 수행
• 이 결과가 복잡한 문제에서 중간 결정들을 최적화하는 StepTool의 효율성을 나타냄

5. Conclusion

• StepTool 기법 제안 → LLM이 여러 도구를 사용하여 복잡한 다중 스텝 문제를 해결하는 능력을 향상시키는 새로운 단계별 강화학습 프레임워크
• 2개의 핵심 요소로 구성
  • Step-grained Reward Shaping: 도구 호출의 성공과 문제 해걸의 기여를 평가
  • Step-grained Optimization: 정책 경사를 사용하여 각 스텝에서 의사 결정을 최적화
• 실험은 3개의 오픈소스 모델을 이용하여 수행 → 문제 해결 성능의 효율성을 확인

Limitations

• PPO 학습 과정이 불안정 할 수 있음
• 좋은 결과를 달성하긴 했지만 아직 더 성능 향상의 여지가 있음
  • 본 논문의 기법은 다수의 라운드에 대한 온라인 데이터 수집과 최적화를 지원하지만 시간과 비용 문제 때문에 단일 라운드에 대한 오프라인 학습만 수행
  • 이는 성능 향상에 대한 모델의 능력을 제한할 수 있음