Stop Regressing: Training Value Function via Classification for Scalable Deep RL

 

• Paper: https://arxiv.org/pdf/2403.03950v1.pdf
• C51 관련 내용을 알고 보면 더 좋을 듯 합니다!

0. Abstract

• 가치함수 (Value Function)은 심층 강화학습에서 중심적인 요소
• 인공신경망으로 파라미터화 된 해당 함수는 bootstrapped 타겟값과 일치하도록 평균 제곱 오차 회귀 목적함수 (Mean squared error regression objective)를 사용하여 학습
• 그러나 이렇게 회귀를 사용하는 가치 기반 강화학습은 큰 규모의 네트워크 (ex. Transformers)로의 확장이 어려움
• 이런 어려움은 지도 학습에 비해 극명하게 드러남 → Cross-entropy 기반의 지도 학습 기법은 대형 네트워크로 확장될 수 있음
• 이에 따라 본 논문에서는 가치 함수의 학습에 회귀 대신 단순히 분류를 사용하는 방식을 통해서 심층 강화학습이 개선될 수 있는지에 대한 확장성을 검증
• 실제 Categorical cross-entropy로 학습된 가치 함수가 다양한 도메인에서 향상된 성능을 보임
  • 확장된 도메인의 종류 → Atari 2600의 단일 작업 RL (with SoftMoEs), 대형 ResNet을 사용한 Atari에서의 다중 작업 RL, Q-transformers를 사용한 로봇 제어, 탐색 없는 체스 플레이, 대용량의 Transformers를 활용한 언어 에이전트의 Wordle 문제
  • 위의 문제들에서 SOTA 성능을 달성
• 또한 Categorical cross-entropy를 사용하는 경우 가치 기반 강화학습이 가지고 있던 문제인 noisy target과 non-stationarity를 해결
• 단순히 가치 함수의 학습을 categorical cross-entropy로 옮김으로서 아주 조금의 비용, 혹은 비용 없이 강화학습의 확장성 측면에서 큰 향상을 달성

1. Introduction

• AlexNet에서 Transformers까지 딥러닝의 발전을 살펴봤을 때 분류 문제의 경우 큰 인공 신경망을 통해 효율적으로 학습이 수행되었음
• 하지만 지도학습의 트렌드와 다르게 가치 기반 강화학습 기법은 주로 회귀 (Regression)에 의존 → 예를 들면 DQN이나 Actor-Critic 같은 기법들은 평균 제곱 오차와 같은 회귀 손실 함수를 사용하고 연속적인 스칼라 타겟값을 통해 가치 함수를 학습
• 이런 회귀 손실함수를 가지는 가치 기반 강화학습 기법은 대용량의 transformers와 같이 큰 네트워크로 확장하는 것이 어려움 → 이런 확장성의 부족은 여러 문제들을 유발
• 그렇다면 단순히 이런 회귀 문제를 분류 문제로 대체하는 것 만으로 지도 학습과 유사한 확장성을 달성할 수 있을까?
• 본 논문에서는 가치 함수를 categorical cross-entropy 손실 함수로 학습하는 방법을 제안 → 해당 방식의 적용을 통해 심층 강화학습 기법의 성능, 강인함, 확장성에 있어서 개선을 확인 (그림 1 참고)
  

  

• 그림 1의 결과는 고전적인 회귀 기반 접근 대신 HL-Gauss cross-entropy 손실함수를 사용했을 때의 결과
  • 성능 향상 결과
    • Mixture-of-Experts (MoE)를 사용한 파라미터 확장을 수행한 Atari 환경의 단일 문제 RL → 30% 성능 향상
    • Atari의 다중 문제 세팅 → 1.8 - 2.1배 성능 향상
    • Wordle 문제에서 언어 에이전트의 성능 → 40% 향상
    • 탐색 없는 체스 문제 → 70% 성능 향상
    • Transformers를 사용한 대규모 로봇 제어 문제 → 67% 성능 향상
• 또한 평균 제곱 회귀 대신 cross-entropy를 사용했을 때 많은 이점을 보임
  • 노이지 타겟에 대한 강인성이 향상되는 것을 확인
  • 큰 용량을 non-stationary 타겟에 대해 더 잘 사용함

2. Preliminaries and Background

Regression as Classification

• 확률적인 관점으로 회귀에 대한 문제 정의
  • 입력: $x \in \mathbb{R}^d$
  • 타겟을 조건부 분포로 모델링: $Y|x \sim \mathcal{N}(\mu=\hat{y}(x;\theta), \sigma^2)$ (고정된 분산 $\sigma^2$)
  • 예측 함수: $\hat{y}: \mathbb{R}^d \times \mathbb{R}^k \rightarrow \mathbb{R}$ (벡터 $\theta \in \mathbb{R}^k$로 파라미터화)
• 데이터 $\{x_i, y_i\}_{i=1}^N$에 대한 maximum likelihood 예측기는 평균 제곱 에러 (Mean-Squared Error, MSE) 목적함수를 가짐
  

  

• 최적의 예측기: $\hat{y}(x;\theta^*) = \mathbb{E}[Y|x]$
• 조건부 분포의 평균을 직접적으로 학습하는 대신 대안적인 접근은 타겟 값에 대한 분포를 학습하고 분포의 통계로 예측 $\hat{y}$를 구하는 것
• 이를 통해 타겟 분포 $Y|x$를 확률 밀도 함수 $p(y|x)$로 구축 → 스칼라 타겟값은 분포 $y=\mathbb{E}_p [Y|x]$의 평균으로 도출
• 이제 회귀 문제를 타겟 $p(y|x)$에 대해서 파라미터화 된 분포 $\hat{p}(y|x;\theta)$에 대한 KL-divergence를 최소화하는 것에 대한 학습으로 생각할 수 있음!!
  

  

  
  
  • Cross-entropy 목적함수!
• 최종적으로 예측을 도출 → $\hat{y}(x;\theta) = \mathbb{E}_{\hat{p}}[Y|x;\theta]$
• 이렇게 새로운 문제 정의가 주어졌을 때 분포에 대한 학습을 다룰 수 있는 손실함수로 변경하기 위해 $\hat{p}$를 서포트 [$v_{min}, v_{max}$]에서 균일한 공간의 위치 혹은 “클래스”를 가지는 ($v_{min} \leq z_1 < ... < z_m \leq v_{max}$) 카테고리 분포 (Categorical Distribution)의 세트로 제한
  

  

  
  
  • $p_i$: 위치 $z_i$에 대한 확률
  • $\delta_{z_{i}}$: $z_i$ 위치에서의 Dirac delta 함수
• 첫번째 허들은 타겟 분포 $Y|x$를 구축하기 위한 과정을 정의하고 카테고리 분포 $\mathcal{Z}$의 세트에 이를 투영 (Projection) 하는 것
• 위 내용은 기존 Distributional RL의 C51 기법의 내용과 유사하다고 생각됨

 

Reinforcement Learning (RL)

• 강화학습 관련 개념들
  • 에이전트가 환경에서 현재 상태 $S_t \in \mathcal{S}$에서 행동 $A_t \in \mathcal{A}$를 취하여 상호작용을 수행하여 환경 변환 확률 (Environment Transition Probability)에 따라 다음 상태 $S_{t+1}$로 이동하며 보상 $R_{t+1}$을 받음
  • 반환값은 행동의 시퀀스에 대한 품질을 정의 → 보상의 감가된 누적 합 → $G_t = \sum_{k=0}^{\infty}\gamma^k R_{t+k+1}$ 이며 $\gamma \in [0,1)$은 감가율 (Discount factor
  • 에이전트의 목표는 기대 반환값을 최대로 하는 정책 $\pi:S \rightarrow\mathcal{P}(A)$를 학습하는 것
  • 행동-가치 함수는 정책 $\pi$가 주어졌을 때 상태 $s$에서 행동 $a$를 취한 경우 기대되는 반환값 → $q_{\pi}(s,a)=\mathbb{E}_{\pi}[G_t |S_t=s, A_t=a]$
• Deep Q Network (DQN)는 최적에 근사하는 상태-행동 가치 함수로 학습을 수행
  • $Q(s,a;\theta) \approx q_{\pi*} (s,a)$ → $\theta$로 파라미터화 된 인공신경망 사용
  • DQN은 데이터셋 $\mathcal{D}$로부터 샘플링 된 $(S_t, A_t, R_{t+1}, S_{t_1})$로부터 계산한 시간차 오차 (Temporal Difference Error, TD-Error)를 최소화 하도록 학습
    

    

    
    
    • $\theta^-$는 파라미터 $\theta$에 대한 느린 이동 복사본 (Slow moving copy)으로 타겟 네트워크를 파라미터화
      

      

    • 이는 벨만 최적 방정식으로 회귀에 대한 스칼라 타겟값을 정의
    • 대부분의 심층 강화학습 알고리즘은 이를 기본으로 하는 다양한 변형을 통해 가치 함수를 정의하고 사용
• 추가적으로 오프라인 강화학습을 통해 고정된 환경 상호작용 데이터셋을 사용하여 에이전트를 학습하는 방법이 있음
  • 대표적인 기법 = CQL → Strength $\alpha$를 포함하는 행동 정규화 (Behavior Regularization) 손실함수로 TD 에러를 최적화
  • 다음과 같은 학습 목적 함수 사용
    

    

• 본 논문의 목표는 이렇게 가치 기반, 액터-크리틱 기반의 기법들에서 기본적으로 사용되는 평균 제곱 TD 에러 목적함수를 분류 형식의 cross-entropy 손실함수로 변경하는 것

3. Value-based RL with Classification

• 이번 섹션에서는 TD 학습의 회귀 문제를 분류 문제로 변환하는 방법에 대해 알아볼 것
  • `스칼라 Q 값과 식 2.3의 TD 타겟사이의 제곱 거리를 줄이는 것 대신 카테고리 분포 사이의 거리를 최소화하는 방법
• 이를 위해 먼저 행동 가치 함수인 $Q(s,a)$에 대한 카테고리 표현 (Categorical Representation)을 정의할 수 있어야 함

Categorical Representation

• 먼저 Q값을 카테고리 분포 $z \in \mathcal{Z}$의 기대값으로 표현
• 이 분포는 각 위치 혹은 “클래스” $z_i$에 대한 확률 $\hat{p}_i (s,a;\theta)$로 파라미터화 → 확률은 logits $l_i (s,a;\theta)$에 대한 소프트 맥스 (Softmax) 함수를 통해 얻음
  

  

• TD 학습에 대한 Cross-entropy 손실함수 (식 2.1) 계산을 위해 타겟 분포 또한 동일한 위치 $z_i, ..., z_m$에 대한 카테고리 분포를 가짐
• 이는 직접적인 cross-entropy 손실함수 연산이 가능하도록 함
  

  

  
  
  • 타겟 확률 $p_i$는 다음과 같이 정의됨 → $\sum_{i=1}^m p_i (S_t, A_t;\theta^-)z_i \approx (\hat{\mathcal{T}}Q)(S_t ,A_t ; \theta)$
• 이제 타겟 확률 $p_i (S_t, A_t ; \theta^-)$의 계산을 위한 2가지 전략을 살펴보자
  

  

 

 

 

3.1. Constructing Categorical Distributions from Scalars

• 먼저 스칼라 타겟 $(\hat{\mathcal{T}}Q)(S_t ,A_t ; \theta)$를 $\{z_i\}_{i=1}^m$의 서포트를 가지는 카테고리 분포에 투영할 수 있어야 함
• 스칼라를 하나 혹은 $m$개의 bin으로 이산화 해야함 ($z_i$는 각 bin의 중간값을 나타냄)
• 이를 원핫 분포로 나타내는 것은 Q 함수에 대해 에러를 유발할 수 있음 → 더 편향된 추론과 나쁜 성능 도출
• 이를 위한 첫번째 기법은 “two-hot” 접근법 → 스칼라 타겟을 타겟이 사이에 위치한 두개의 위치에 두개의 0이 아닌 밀도로 확률 분포를 나타내는 것 (그림 3의 왼쪽 참고)

A Two-Hot Categorical Distribution

• $z_i, z_{i+1}$을 TD 타겟의 상한과 하한 값으로 설정 → $z_i \leq (\hat{\mathcal{T}}Q)(S_t ,A_t ; \theta) \leq z_{i+1}$
• 해당 위치들의 확률 $p_i$와 $p_{i+1}$은 다음과 같이 계산
  

  

• 모든 다른 위치들에서 카테고리 분포의 확률은 0으로 설정
• Two-Hot 변환은 스칼라 TD 타겟을 카테고리 분포로 나타낼 때 식별 가능하고 손실이 없는 표현을 제공
• 그러나 Two-Hot은 이산 회귀의 서수 구조 (Ordinal struction)를 완전히 활용하지 않음 → 클래스가 독립적이지 않고 클래스가 본질적으로 이웃 클래스와 연관되는 순서를 가짐
• Histogram Losses 클래스는 인접한 bin에 확률 질량 (Probability mass)를 분배하여 회귀 문제의 서수 구조를 활용 → 지도 분류의 라벨 smoothing과 유사
• 이는 노이지한 타겟값을 확률 질량이 두개의 위치에 제한되는 것이 아니라 타겟 주변의 여러 bin으로 확장된 카테고리 분포로 변환하는 방법 → 그림 3의 중간 그림 참고

 

Histograms as Categorical Distributions (HL-Gauss)

• 랜덤 변수 $Y|S_t , A_t$를 확률 밀도 $f_{Y|S_t , A_t}$와 기대값 $(\hat{\mathcal{T}}Q)(S_t ,A_t ; \theta)$를 가지는 누적 분포 함수 $F_{Y|S_t, A_t}$로 정의
• 분포 $Y|S_t, A_t$를 $z_i$를 중심으로 하며 너비 $\varsigma=(v_{max}-v_{min})/m$을 가지는 bin의 히스토그램에 투영 → 확률을 얻기 위해 구간 $[z_i - \varsigma/2 , z_i + \varsigma/2]$에 대해 적분
  

  

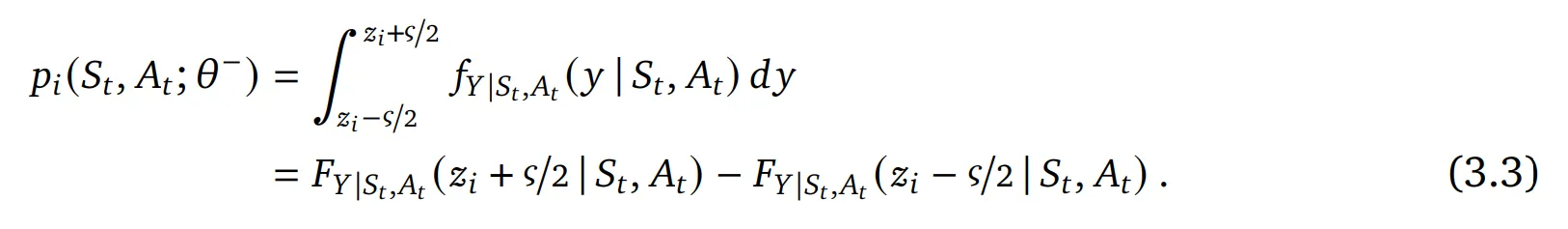
• 이제 분포 $Y|S_t, A_t$에 대한 선택을 해야함 → 가우시안 분포 $Y|S_t, A_t \sim \mathcal{N}(\mu=(\hat{\mathcal{T}}Q)(S_t ,A_t ; \theta), \sigma^2)$을 사용할 때 분산 $\sigma^2$은 카테고리 분포의 라벨 smoothing을 조절하기 위한 하이퍼 파라미터로 사용

 

How should we tune $\sigma$ in practice?

• HL-Gauss는 표준 편차 $\sigma$와 추가적으로 bin의 너비 $\varsigma$와 분포의 범위 $[v_{min}, v_{max}]$에 대한 튜닝을 수행해야함
• 표준 정규 분포로부터 샘플링 한 99.7%가 평균의 3 표준 편차 이내에 높은 확신을 가지고 위치함 → $6 \cdot \sigma / \varsigma$ bin에 근사
• 더욱 해석 가능한 하이퍼 파라미터로 추천하는 것은 $\sigma/ \varsigma$로 튜닝하는 것 → 이를 $K/6$으로 설정하는 경우 대부분의 확률 질량이 $[K]+1$ 이웃의 위치에 분포
• 본 논문의 실험에서는 $\sigma / \varsigma = 0.75$로 튜닝 → 거의 6개의 위치에 대해 질량이 분포하도록 함

3.2. Modelling the Categorical Return Distribution

• 이전 섹션에서는 기대 반환값을 나타내는 스칼라 회귀 타겟으로부터 타겟 분포를 만드는 방법에 대해 살펴봤음
• 다른 선택지는 distributional RL처럼 카테고리 모델 $Z$를 사용하여 미래 반환값에 대한 분포를 직접적으로 모델링 하는 것
• 특히 distributional RL의 초기 기법 중 하나인 C51의 경우 예측 분포 $Z$와 TD 타겟의 분포 사이의 cross-entropy를 최소화하는 카테고리 표현 사용
• 이에 따라 C51의 기법도 타겟 분포의 cross-entropy 목적함수를 구하기 위한 Two-Hot이나 HL-Gauss의 대안 기법으로 고려

Categorical Distributional RL

• 카테고리 반환값 분포를 모델링 하기 위한 첫 단계는 $Z$에 대한 확률적 분포 벨만 연산자(Stochastic distributional Bellman operator)를 정의하는 것
  

  

  
  
  • $A_{t+1}=\argmax_{a'}Q(S_{t+1}, a')$
• 확률적 분포 벨만 연산자는 카테고리 투영 과정에서 위치 $z_i$가 이동하고 확장되는 (scaling) 것의 영향을 받음
• 해당 투영은 확률을 이웃의 위치들과의 거리에 비례하여 값을 분배 → $z_{j-1} \leq R_{t+1} + \gamma z_i \leq z_j$ (그림 3의 오른쪽 참고)
• 이웃 위치들을 식별하기 위해 $\lfloor x \rfloor = argmax \{z_i : z_i \leq x\}$와 $\lceil x \rceil = argmin\{z_i : z)i \geq x\}$로 정의
• 위치 $z_i$의 확률을 다음과 같이 도출
  

  

4. Evaluating Classification Losses in RL

• 본 실험의 목표는 섹션 3에서 논의한 다양한 타겟 분포에 categorical cross-entropy 손실함수를 적용했을 때 다양한 문제에서 가치 기반 강화학습의 성능과 확장성의 향상을 살펴보는 것
• 아타리 2600에서의 단일, 다중 RL 문제, 언어 에이전트, 체스, 로봇 제어 등의 문제에서 성능 검증 (온라인, 오프라인)

4.1. Single-Task RL on Atari Games

• 먼저 HL-Gauss, Two-Hot, C51의 유효성을 Arcade Learning 환경에서 검증
• 회귀에 대한 베이스라인으로 DQN을 평균 제곱 에러 TD 목적함수로 학습
• 각 기법은 Adam optimizer로 학습

Evaluation

• 평가 지표: 95% stratified bootstrap confidence intervals (CIs)를 가지는 interquartile mean (IQM) 정규화 점수 → 다수의 시드로 다회 검증
• 온라인 RL에 대해서는 60개의 아타리 게임에 대해 human-normalized aggregated 점수를 사용
• 오프라인 RL에 대해서는 17개의 게임에 대해 behavior-policy normalized 점수 사용

Online RL results

• 앞서 언급한 회귀 손실함수를 사용하는 DQN으로 200M 프레임에 대해서 학습
• 60개의 아타리 게임에서 aggregated human-normalized IQM 성능과 최적화 갭 (optimality gap)을 사용 → 그림 4의 왼쪽 참고
  

  

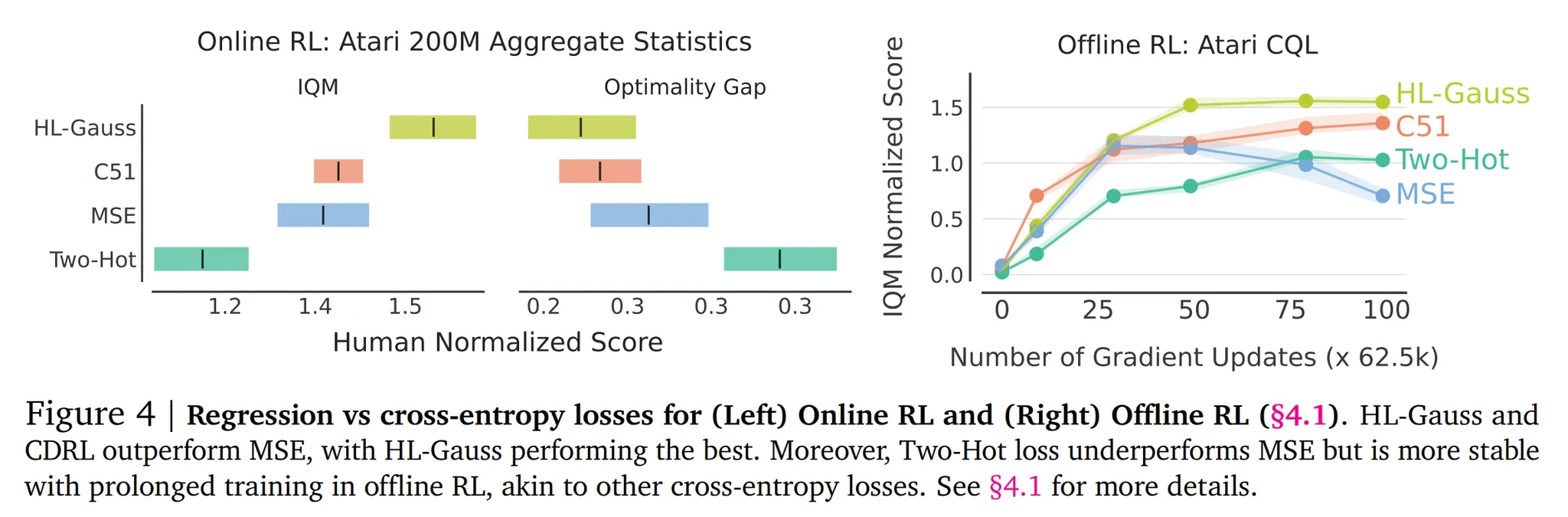
• HL-Gauss가 Two-Hot이나 MSE 손실함수의 성능을 능가하는 것을 확인!
• 반환값 분포에 대한 모델링을 하지 않았음에도 카테고리 분포 RL인 C51보다도 향상된 성능을 보임
  • 이를 통해 반환값 분포에 대한 모델링과 비교했을 때 손실함수 (cross-entropy)가 C51에 더 중요한 요소라고 가정할 수 있음

 

Offline RL results

• 오프라인 데이터셋에서도 이런 학습 방법이 효율적일까?
• 아타리 DQN의 리플레이 데이터셋의 10%에 대해 다른 손실함수로 학습 → CQL을 통해 6.25M gradient 스텝만큼 학습
• 그림 4의 오른쪽을 보면 HL-Gauss와 C51이 지속적으로 MSE의 성능을 능가하는 것을 확인
• Two-Hot의 경우 MSE보다 더 안정적인 성능을 보이지만 다른 두 분류 기법에 비해서는 낮은 성능을 보임
• 또한 평균 제곱 회귀 손실함수를 사용하는 경우 지속적인 학습에 따라 성능이 감소하지만 cross-entropy 손실함수를 사용하는 경우 (HL-Gauss, C51) 해당 성능 감소 없이 안정적

4.2. Scaling Value-based RL to Large Networks

• 지도학습, 특히 언어 모델에서는 네트워크의 파라미터가 늘어날수록 일반적으로 성능이 향상됨
• 하지만 이런 가치 기반 강화학습 기법에서는 단순한 모델 확장이 성능 저하로 이어질 수 있음
• 이에 따라 본 논문에서는 심층 RL의 MSE 회귀 손실함수 대신 분류 기법을 사용했을 때의 효율성을 살펴보고 가치 네트워크의 파라미터 스케일에 따라 성능 향상이 가능하도록 할 것

4.2.1. Scaling with Mixture-of-Experts

• 최근 Obando-Ceron et al. (2024)에서는 아타리에서 단일 문제 RL을 풀때 CNN 네트워크를 확장하는 경우 성능 저하가 있을 수 있지만 Mixture-of-Experts (MoE)를 해당 네트워크에 적용했을 때는 성능이 향상되는 것을 확인
• 이에 따라 본 논문에서는 Impala의 penultimate 층을 SoftMoE로 변경하고 experts의 수를 {1, 2, 4, 8}로 테스트
• 본 논문에서 변경한 유일한 점은 SoftMoE DQN의 MSE 손실함수를 HL-Gauss cross-entropy 손실함수로 변경한 것 → 그림 5 참고
  

  

• 그림 5를 보면 HL-Gauss가 expert 수의 증가에 따라 지속적으로 성능이 향상되는 것을 확인할 수 있음
• SoftMoE + MSE의 경우 MSE에 비해서 확장에 대한 부정적인 영향은 덜 받는 것으로 보임
  • 이는 SoftMoE + MSE에서 사용하는 소프트맥스 때문에 분류의 손실함수를 사용한 것과 유사한 영향을 준 것으로 생각됨

 

4.2.2. Training Generalist Polices with ResNets

• 아타리 환경에서 비디오 게임을 플레이하는 일반적인 정책을 학습하기 위해 온라인과 오프라인 기법 모두에 대해 가치 기반 ResNet의 확장을 고려
• 다중 문제 (Multi-task) RL을 위한 Q 네트워크의 사이즈를 다양화하며 학습을 수행하고 네트워크 크기에 따른 성능을 확인

Multi-task Online RL

• 아타리에서 다중 문제 정책을 학습하기 위해 환경의 역학과 보상을 변경한 변형들을 생성
• 2개의 아타리 게임에서 평가 수행 → Asteroids에 대해 63개의 변경, Space invaders에 대해 29개의 변형 사용
• 강화학습 알고리즘은 분산 액터-크리틱 기법인 IMPALA를 사용하고 MSE 가치 손실함수와 cross-entropy 기반 HL-Gauss 손실함수를 비교
• 네트워크의 확장은 Impala-CNN (≤2M 파라미터)에서 ResNet-101 (44M 파라미터)까지 테스트
• 15B 프레임에 대해 학습 수행하고 5개의 시드로 실험을 반복
• Asteroids의 결과는 그림 6에서 확인 가능하며 Space Invaders의 결과를 그림 D.3에서 확인 가능
  

  

  

  
  
  
• 두 환경 모두에서 HL-Gauss가 MSE보다 더 좋은 성능을 보임
• 특히 Asteroids에서는 ResNet-18 이후부터는 MSE의 성능이 하락하는 것을 확인할 수 있음

Multi-game Offline RL

• Kumar et al. (2023)과 동일한 세팅을 사용 → Distributional C51 대신 non-distributional HL-Gauss 손실함수를 사용하도록 변경
• 하나의 일반화된 정책으로 40개의 아타리 게임을 동시에 플레이하도록 학습
• 데이터셋: 최적에 가까운 학습 데이터셋 사용 → 각 환경에서 독립적으로 학습된 온라인 강화학습 에이전트로 수집한 데이터 사용
• 다중 게임 RL 환경의 셋업은 Lee et al. (2022)에서 제안한 것을 사용하며 디자인적인 선택 (e.g. 특징 정규화, 네트워크 사이즈)을 동일하게 사용
• 그림 7을 확인하면 HL-Gauss로 네트워크를 확장하는 것이 C51을 통한 확장보다 좋은 성능을 보이는 것을 확인할 수 있음
  

  

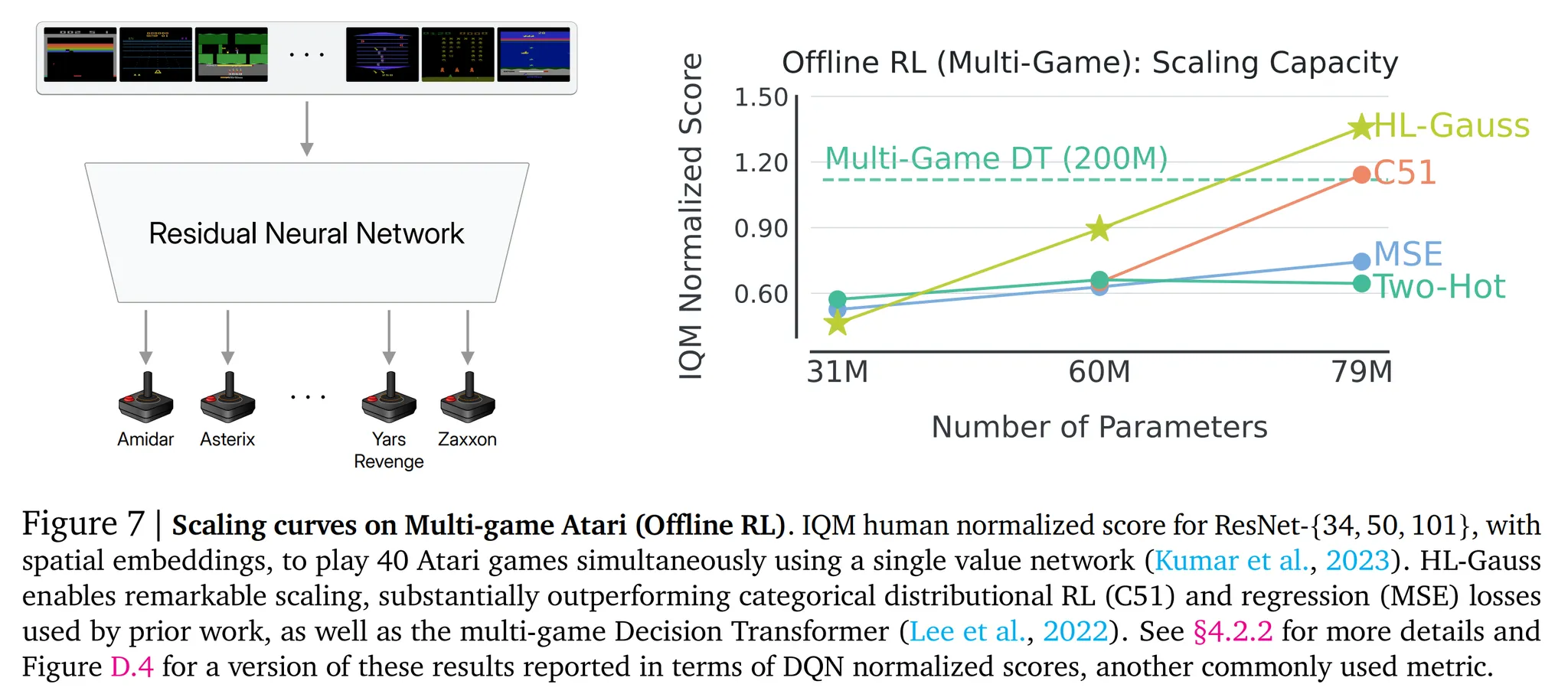
• 기존에 가장 좋은 성능을 보인 ResNet-101 (80M 파라미터)에서 IQM human normalized 점수로 45% 정도의 성능 향상을 보임
• MSE 회귀 손실함수의 경우 ResNet-34 보다 네트워크가 확장되어도 성능은 정체되는 것을 확인
• 이를 통해 HL-Gauss를 사용했을 때의 성능 향상과 분류 기반 cross-entropy 손실함수를 사용했을 때의 유효성을 확인

 

4.3. Value-based RL with Transformers

• 이제 아타리 환경 외에 다른 환경에서도 HL-Gauss의 성능을 평가 → 다수의 문제에서 높은 용량을 가지는 트랜스포머 네트워크를 사용
• 적용 문제들: Wordle 문제를 위한 언어 에이전트, 추론시 탐색 없이 체스를 플레이하는 에이전트, 로봇 제어 에이전트

4.3.1. Language Agent: Wordle

• 언어 에이전트 벤치마크에서 분류 손실함수를 사용했을 때 가치 기반 강화학습의 성능을 평가
• Wordle 게임에서 HL-Gauss와 MSE의 성능을 비교
• Wordle 환경과 그 특징
  • 단어를 추론하는 게임으로 에이전트는 6번의 시도를 할 수 있음
  • 각 턴에서 에이전트는 추론한 글자들이 실제 단어인지에 대한 피드백을 환경으로부터 받게 됨
  • 해당 환경의 역학은 비-결정적 (non-deterministic)
• 실험은 오프라인 RL 세팅으로 진행 → 차선의 (suboptimal) 환경 플레이 데이터셋은 Snell et al. (2023)을 사용
• 해당 실험의 목표는 Q 네트워크를 대신하는 125M 파라미터의 GPT와 같은 디코더만 있는 트랜스포머를 학습하는 것
• 어떻게 트랜스포머 모델이 해당 게임에서 사용되었는지는 그림 8의 왼쪽을 참고
  

  

• DQN의 Q-learning 업데이트와 CQL 스타일의 behavior regularizer를 결합한 오프라인 RL 방식으로 20K gradient 스텝 동안 언어 기반 트랜스포머를 학습 → 다음 토큰 예측 손실함수 사용
• 그림 8의 오른쪽과 같이 다양한 CQL 정규화 strength 계수 조절에 대해서 HL-Gauss가 MSE의 성능을 능가하는 것을 확인

4.3.2. Grandmaster-level Chess without Search

• 트랜스포머는 지식 증류 (Distillation)을 통해 추론 연산 시간을 효과적으로 줄이는 범용 알고리즘의 근사 모델 (Approximator)로서의 효과를 입증
• 이에 따라 HL-Gauss를 통해 스칼라 행동 가치가 아닌 분류 타겟 가치 함수를 증류하도록 학습
• 트랜스포머를 사용하여 Stockfish 16 (복잡한 휴리스틱과 외부 탐색을 조합한 가장 강력한 체스 엔진)의 행동 가치 함수의 증류에 대한 HL-Gauss 성능 평가
• 증류 데이터셋은 Stockfish 엔진으로 얻은 10M개의 체스 게임 데이터로 구성 → 15B개의 데이터 (그림 9의 왼쪽 참고)
  

  

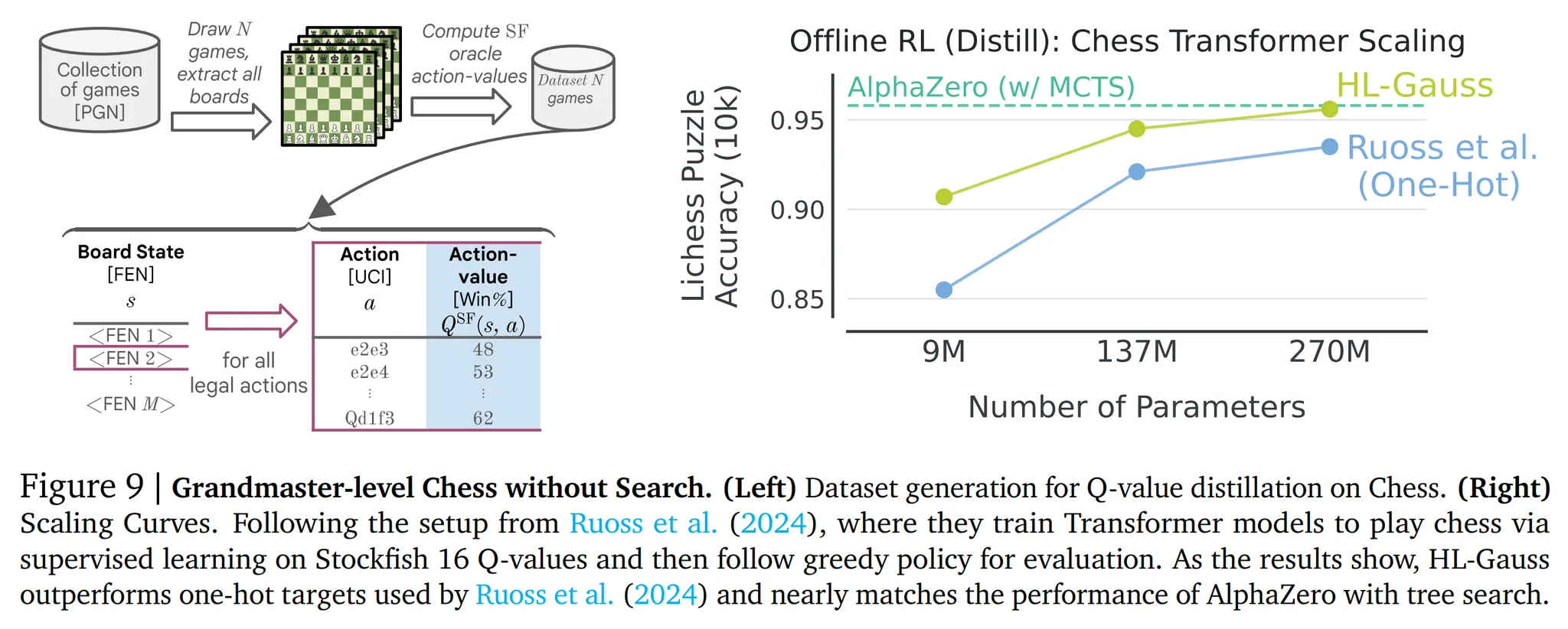
• 다른 크기를 가지는 3개의 트랜스포머 학습 (9M, 137M, 270M 파라미터)
• HL-Gauss와 1-hot 분류 타겟 사용 → 1-hot 분류 타겟이 더 좋은 성능을 보이므로 MSE는 생략
• 각 모델의 성능은 10,000개의 체스 퍼즐을 푸는 능력으로 평가했으며 알려진 풀이와 비교했을 때의 정확도를 사용
• 그림 9의 오른쪽을 확인해보면 270M 트랜스포머를 사용한 1-hot 타겟이 탐색 없는 알파제로 베이스라인의 성능을 뛰어넘으며 HL-Gauss는 더 강력한 400 MCTS 시뮬레이션을 사용한 알파제로와의 성능 격차를 줄임

 

4.3.3. Generalist Robotic Manipulation with Offline Data

• Cross-entropy 손실함수가 대규모의 비전 기반 로봇 제어 문제에서 성능을 향상시킬 수 있는지 평가
• 주방용 조리대가 앞에있는 7 자유도의 모바일 조작 로봇의 시뮬레이션 사용
• 목표는 해당 로봇을 조작하여 랜덤 초기 위치, 방해하는 물체 등이 있는 상황에서 17개의 다른 주방 용품을 성공적으로 잡아서 들어올리는 것
• 500,000개의 데이터셋 사용 → 40,000개의 에피소드
• 60M 파라미터를 가지는 Q-Transformer 모델 사용
• Chebotar et al. (2023)의 기법을 사용하지만 MSE 회귀 손실함수를 HL-Gauss 분류 손실함수로 변경
• 그림 10을 통해 볼 수 있듯이 HL-Gauss가 회귀 베이스라인에 비해서 67% 높은 성능을 보이며 더 샘플 효율적임을 알 수 있음
  

  

5. Why Does Classification Benefit RL?

• 본 논문의 실험을 통해 분류 손실함수가 가치 기반 심층 강화학습 알고리즘의 성능과 확장성 향상에 기여하는 것을 보임
• 또한 categorical cross-entropy 손실함수가 가치 기반 강화학습이 겪는 몇가지 어려운 점들을 해결할 수 있다는 점을 이해 → 표현 학습 (Representation learning), 안정성, 강인성
• 또한 ablation 실험을 통해 HL-Gauss가 왜 다른 카테고리 타겟들에 비해 우수한지 이유를 검증

5.1. Ablation Study: What Components of Classification Losses Matter?

• 본 논문에서 사용한 분류 손실함수가 기존 가치 기반 강화학습에서 사용하는 전통적인 회귀 손실함수와 다른 점
  • 가치 네트워크의 출력을 파라미터화 → 스칼라 대신 카테고리 분포를 취득
  • 스칼라 타겟을 카테고리 타겟으로 변환하는 전략

5.1.1. Are Categorical Representations More Performant?

• 본 논문에서는 Q 네트워크를 파라미터화 하고 logits 출력을 소프트맥스 연산을 통해 카테고리 분포의 확률로 변환
• 소프트맥스는 Q 값과 출력의 gradient를 제한 → 강화학습의 학습 안정성을 향상시킴
• Cross-entropy 손실함수의 사용 없이 Q 값의 파라미터화만이 미치는 영향을 알기 위해 Q 함수에 동일한 파라미터화를 적용하지만 MSE를 사용
• 이 경우 온라인 (그림 11)과 오프라인 (그림 12) 모든 경우 성능 향상이 이루어지지 않았음을 알 수 있음 → 중요한 것은 cress entropy 손실함수를 사용하는 것!
  

  

5.1.2. Why Do Some Cross-Entropy Losses Work Better Than Others?

• HL-Gauss와 Two-Hot 모두 cross-entropy 손실함수를 사용하지만 HL-Gauss의 성능이 더 뛰어난 이유는 뭘까?
• 2가지 이유가 있을 것으로 가정
  • HL-Gauss는 이웃 위치로 확률 질량을 퍼트리므로 오버피팅을 감소시킴
  • HL-Gauss는 타겟 값의 특정 범위로 일반화
• 첫번째 가정은 분류 문제에서 라벨 smoothing이 오버피팅을 완화하는 것과 동일할 것으로 생각됨
• 이를 13개의 아타리 게임에서 온라인 RL 세팅으로 검증
  • $[v_{min}, v_{max}]$는 고정하고 카테고리 bin들의 수를 다양화 → {21, 51, 101, 201}
  • bin의 너비 $\varsigma$에 대한 편차 $\sigma$의 비율 다양화 → {0.25, 0.5, 0.75, 1.0, 2.0}
• $\sigma$ 값의 넓은 범위에서 HL-Gauss가 Two-Hot의 성능을 능가하는 것을 확인
  • 확률을 주변 위치에 많이 퍼트릴수록 오버피팅이 감소하므로
• 두번째 가정 → 최적의 $\sigma$ 값은 bin의 수와 독립적으로 보임 → HL-Gauss가 타겟값의 특정 범위에 걸쳐 일반화를 수행하고 있음을 나타내며 실제 회귀 문제의 서수적 특성을 활용하고 있습니다. (원문: HL-Gauss generalizes best across a specific range of target values and is indeed leveraging the ordinal nature of the regression problem)

5.2. What Challenges Does Classification Address in Value-based RL?

• 가치 기반 강화학습의 어떤 어려운 점들을 cross entropy 손실함수가 해결하거나 경감시킬 수 있는지 확인해보자

5.2.1. Is Classification More Robust to Noisy Targets?

• 분류는 회귀에 비해 노이지한 타겟에 대한 오버피팅에 덜 취약함
  • 정확한 숫자적인 관계가 아니라 입력과 타겟 사이의 확률적 관계에 집중하므로!
  • 이에 따라 분류가 RL의 확률성에 의해 발생하는 노이즈를 더 잘 다루는지 확인할 것!

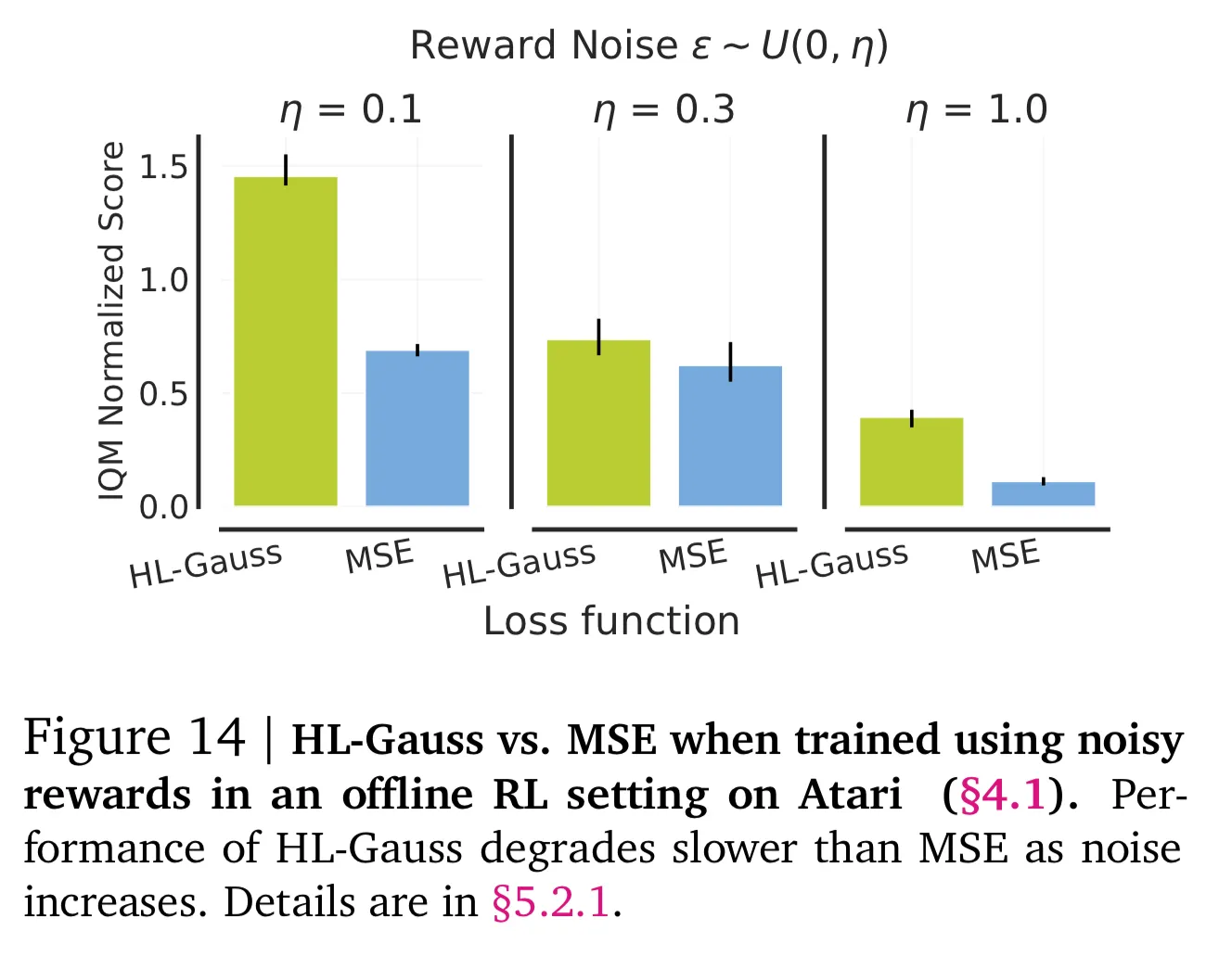
(A) Noisy Rewards

• 보상이 확률적일때 강인성 테스트
• 오프라인 강화학습 설정에서 각 데이터셋의 보상 $r_t$에 $(0,\eta)$에서 균일하게 샘플링한 랜덤 노이즈 $\epsilon_t$를 더함
• 노이즈의 범위는 $\eta \in \{0.1, 0.3, 1.0\}$으로 설정하고 cross-entropy 기반의 HL-Gauss와 MSE 손실함수 사이의 성능 비교
• 그림 14와 같이 노이즈의 범위가 커짐에 따라 HL-Gauss의 성능 저하가 MSE에 비해 더 적음을 알 수 있음
  

  

(B) Stochasticity in Dynamics

• 아타리 실험에서 sticky 행동을 사용 → 25%의 확률로 기존의 행동을 반복하도록 함 → 비결정적 (non-deterministic) 역학을 가지게 됨
• 해당 sticky 행동을 끈 결정적인 아타리 (60개 게임)에서 다른 손싫마수들의 성능을 비교
• 그림 15에서 볼 수 있듯이 cross-entropy 기반의 HL-Gauss가 확률적인 환경에서 MSE의 성능을 능가하는 것을 알 수 있음
• 결정적인 역학보다 조금 떨어지는 성능을 가지고 C51보다 좋은 성능을 보임
  

  

• 위의 결과들을 통해 cross-entropy 손실함수를 사용하는 것이 확률적인 역학이나 보상 등으로 강화학습 환경이 유발하는 노이지한 타겟에 덜 오버피팅하는 것에 기여하는 것을 알 수 있음
• 이를 통해 실제 강화학습 환경에서 역학에 대한 오차나 행동의 지연으로 발생하는 문제에 cross-entropy 손실함수를 사용하는 것이 좋을 것으로 예상됨

5.2.2. Does Classification Learn More Expressive Representations?

• MSE 손실함수만 사용하는 것은 가치 기반 강화학습에서 유용한 표현 (Representation)을 만들어내지 못하는 것으로 알려지며 낮은 용량의 표현 (low capacity representation)을 유발함
• 이는 학습 동안 타겟 값에 충분히 피팅하지 못하는 원인이 될 수 있음
• 스칼라 타겟 대신 카테고리 분포를 예측하는 것이 더 나은 표현을 만들어낼 수 있음
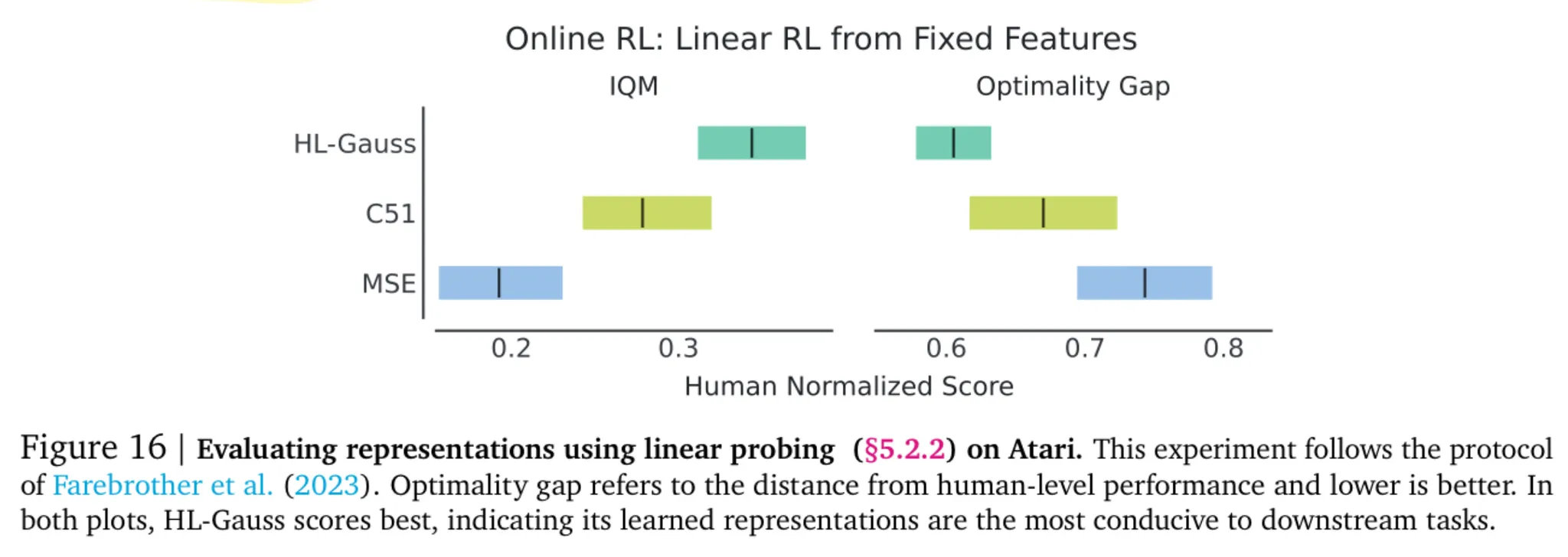
• 이에 대한 검증을 위해 200M 프레임의 아타리 데이터를 사용하여 온라인으로 학습된 가치 네트워크를 취득
  • 해당 네트워크의 표현을 고정시키고 단일 선형 레이어를 추가하고 Q 함수를 다시 학습하며 이를 통해 정책을 처음부터 학습 수행
  • 그림 16에서 볼 수 있듯이 cross-entropy 손실함수가 더 좋은 결과를 보이는 것을 알 수 있음
  • 처음부터 정책을 학습했을 때의 성능 향상을 보았을 때 가치를 통해 더 나은 표현이 학습되었음을 알 수 있음

5.2.3. Does Classification Perform Better Amidst Non-Stationary?

• 가치 기반 RL의 타겟 계산은 지속적으로 변하는 argmax 정책과 가치 함수로 인해 non-stationarity 성격을 가짐
• C51 논문에서는 분류 기법이 이런 non-stationarity 정책의 어려움을 해결할 수 있을 것으로 가정했지만 이를 검증하지는 못했음
• 본 논문에서는 분류가 회귀보다 더 타겟의 non-stationarity를 잘 다루는 것을 보임

Synthetic Setup

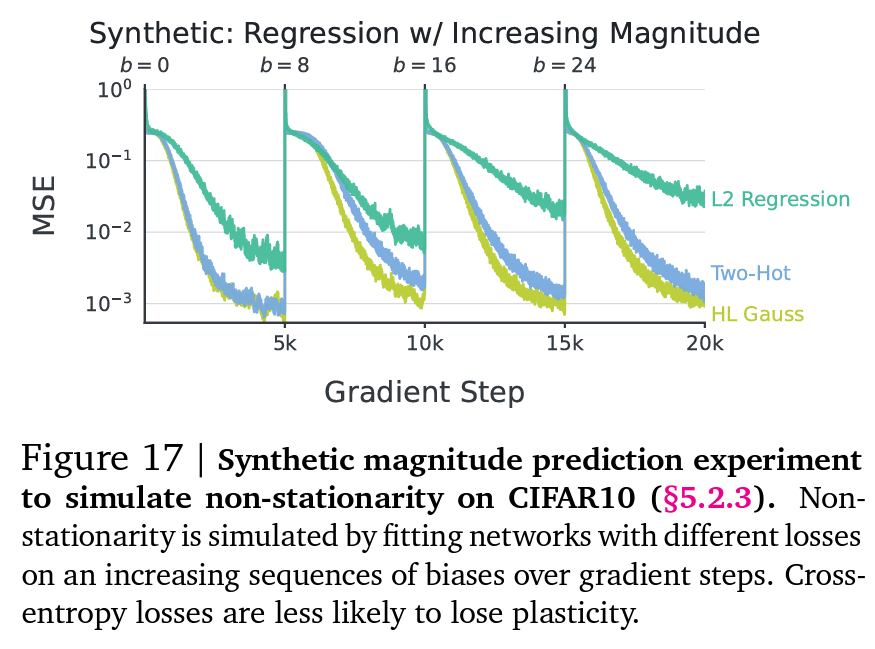
• 먼저 CIFAR 10에 대해 인공적인 회귀 문제를 정의
  • 입력 이미지 $x_i$가 랜덤하게 초기화 된 인공신경망 $f_{\theta^-}$를 통과하여 회귀 타겟으로 맵핑 → 높은 주기의 타겟 생성: $y_i = \sin (10^5 \cdot f_{\theta^-}(x_i))+b$
  • $b$는 상수인 편향으로 타겟의 크기를 제어
• TD를 통해 가치 함수를 학습할 때 예측 타겟은 non-stationary이며 시간이 지남에 따라 정책이 개선되며 값이 증가
• 다른 손실함수를 사용하는 인공신경망들을 통해 해당 세팅을 시뮬레이션 → 편향 $b \in \{0, 8, 16, 24, 32\}$로 사용
• 그림 17에서 볼 수 있듯이 분류 손실함수는 회귀에 비해 non-stationary 타겟 하에서 더 큰 유연성을 가짐
  
  

Offline RL

• 강화학습에서 non-stationary를 제어하기 위해 오프라인 SARSA를 사용 → 고정된 데이터 수집 정책으로 가치를 예측
• 다음 상태 $S_{t+1}$에 대한 학습된 Q 값을 최대화하는 행동을 사용하는 Q 러닝과 대조적으로 SARSA는 오프라인 데이터에서 다음 시간 스텝에서 관측된 행동을 사용 $(S_{t+1}, A_{t+1})$
• 그림 18에서 볼 수 있듯이 MSE와 비교했을 때 HL-Gauss가 가지던 대부분의 장점이 오프라인 SARSA 세팅에서는 사라짐 → 이를 통해 분류 기반 기법이 가치 기반 강화학습의 non-stationary를 더 잘 다루는 것을 알 수 있음
  

  

To summarize

• 위 내용들을 통해 cross-entropy 손실함수는 사용하는 경우 가치 기반 강화학습에서 좋은 성능을 달성하는 것을 알 수 있음
• 가치 기반 강화학습의 많은 문제들을 해결
  • Non-stationarity를 더 잘 대응
  • 매우 높은 표현력을 가짐
  • 노이지한 타겟 값에 대해 강인성을 가짐

6. Conclusion

• 본 논문에서는 평균 제곱 오차 대신 카테고리 cross entropy를 사용하여 회귀 문제를 분류 문제로 치환 → 가치 기반 기법을 다양한 문제에서 성능과 확장성 측면에서 큰 개선을 보임
• 해당 대선들의 원인을 분석했으며 cross entropy가 가치 기반 강화학습에서 더욱 풍부한 표현과 노이즈, non-stationary 측면에서 개선됨을 보임
• 이런 카테고리 cross-entropy의 사용으로 이론이나 실제적 모두에서 심층 강화학습의 알고리즘 디자인이 달라질 것으로 생각함
• 기존 강화학습의 경우 트랜스포머 같은 구조를 사용했을 때 가치 함수를 확장하거나 변경하는 것이 어려웠지만 분류 기법을 적용하면서 가치 기반 강화학습에서 트랜스포머를 적용할 수 있는 자연스러운 접근이 되었음

Appendix

A. Reference Implementations

• HL-Gauss의 Jax와 Pytorch 구현 코드