Planning with Diffusion for Flexible Behavior Synthesis

• Paper: https://proceedings.mlr.press/v162/janner22a/janner22a.pdf
• Blog: https://diffusion-planning.github.io/

0. Abstract

• 기존의 Model-based RL 기법
  • Dynamics model을 근사하기 위한 추정을 목적으로만 학습을 수행하고 의사 결정에 대한 나머지 부분은 고전적인 trajectory optimizer에게 떠넘김
  • 이런 결합은 컨셉적으로는 단순하지만 결점을 가지고 있음 → 학습된 모델이 표준적인 trajectory optimization과 맞지 않을 수 있음
• 본 논문의 제안
  • 본 논문에서는 최대한 trajectory optimization 파이프라인을 modeling 문제에 섞는 방법을 제안 → model로부터의 샘플링과 이를 사용한 planning이 거의 동일하도록 함
  • 본 논문의 핵심적인 기술적 접근 → diffusion probabilistic model → 반복적으로 경로를 denoising하여 planning을 수행
  • 본 논문에서는 classifier-guided sampling과 image inpainting이 어떻게 coherent planning strategies로 재해적될 수 있는지 보여줌
  • 그리고 diffusion-based planning의 특별하고 유용한 특성들에 대해 설명
  • 그리고 본 논문의 기법이 control setting에서 특별한 것을 보임 → 다음의 두가지 사항 강조
    • Long-horizon decision-making
    • test-time flexibility

1. Introduction

• 학습된 모델을 통한 planning은 강화학습이나 데이터 기반 의사 결정에서는 개념적으로 단순한 프레임워크
  • 해당 기법은 지도 학습으로 알지 못하는 환경의 dynamics를 근사하도록 학습
  • 이후에 이 학습된 모델은 고전적인 trajectory optimization 기법에 결합됨
• 그러나 이 조합은 생각대로 잘 작동하지 않음
  • 강력한 trajectory optimizer가 학습된 모델을 활용 → 이 과정에 따라 생성된 plan은 종종 optimal trajectory 보다는 adversarial 한 예시처럼 보임
  • 결과적으로 모델 기반 강화학습 알고리즘은 종종 trajectory optimization 기법보다 value functions, policy gradient 같은 model-free 기법들을 많이 상속 받음
  • Online planning에 의존하는 기법들은 앞에서 언급한 문제들을 피하기 위해 random shooting, cross-entropy method와 같은 단순한 gradient-free trajectory optimization 기법을 사용
• 본 논문에서는 data 기반의 trajectory optimization을 수행하는 새로운 접근 제안
• 핵심 아이디어는 모델로부터의 샘플링과 이를 통한 planning을 거의 동일하게 하는 것!
  • 예를 들어 모델은 궁극적으로는 planning에 사용되기 때문에 행동 분포는 state dynamics 만큼 중요하고 long-horizon accuracy는 single-step error보다 더 중요함
  • 반면에 모델은 보상함수와 무관해야 함 → 학습 도중에 본 적이 없는 다수의 task에서 사용될 수 있도록!
  • 마지막으로 모델은 예측 뿐 아니라 planning이 경험을 통해 개선되고 표준의 shooting based planning 알고리즘의 myopic failure에 저항하도록 해야함
• 본 논문의 아이디어! → Trajectory-level diffusion probabilistic model ⇒ Diffuser (Fig. 1 참고)
  • 일반적인 model-based planning 기법은 시간에 대해 autoregressive하게 예측을 수행하지만 Diffuser는 planning의 모든 timestep에 대해 동시에 예측 수행
  • Diffusion model의 iterative sampling process의 장점 → flexible conditioning → trajectory를 recover할 때 auxiliary guide를 통해 sampling 과정을 변경 → 높은 return을 가지는 trajectory나 constraints들을 만족하는 trajectory 생성 가능
• 본 논문의 기법이 가지는 특징
  • Long-horizon scalability
    • Diffuser는 단일 step 에러보다는 생성되는 경로의 정확도를 위해 학습됨 → 이에 따라 단일 스텝 dynamics model의 누적된 rollout error로 인해 고통받지 않고 long planning horizon으로의 확장이 용이함
  • Task compositionality
    • 보상 함수는 plan을 샘플링 할 때 사용하기 위한 추가적인 gradient를 제공 → 다양한 보상을 동시에 그들의 gradients에 한꺼번에 더함으로써 직접적인 planning이 가능
  • Temporal compositionality
    • Diffuser global하게 연관된 경로들을 생성 → local consistency를 반복적으로 개선하는 방식을 사용
    • 분포 내의 subsequence 들을 연결하여 새로운 궤적들을 일반화할 수 있음
  • Effective non-greedy planning
    • Model과 planner 사이를 모호하게 함으로써 model의 예측을 향상하는 것이 planning 능력의 향상에 영향을 미침
    • 이를 통해 planner의 학습이 long-horizon, sparse-reward problems와 같은 기존의 많은 planning method에서는 해결이 어려웠던 종류의 문제들을 풀 수 있게 함

2. Background

2.1. Problem Setting

• Discrete-time dynamics에 의한 시스템
  • $s_{t+1}=f(s_t, a_t)$, 상태 $s_t$에서 주어진 행동 $a_t$
• Trajectory optimization은 per-time step 보상 (혹은 비용) $r(s_t, a_t)$로 나눠지는 objective $J$를 최대화 (혹은 최소화)하는 행동의 sequence $a_{0:T}^*$를 찾는 것!

• T: planning horizon
• $\tau = (s_0, a_0, s_1, a_1, ..., s_T, a_T)$는 trajectory
• $J(\tau)$: trajectory에 대한 objective value

2.2. Diffusion Probabilistic Models

• Diffusion probabilistic model은 반복적인 denoising 과정 $p_{\theta}(\tau^{i-1}|\tau^i)$을 통해 데이터를 생성하는 기법
• Denoising은 노이즈를 추가하여 데이터의 구조를 천천히 손상시키는 forward diffusion process $q(\tau^i | \tau^{i-1})$를 역으로 수행하는 과정
• 모델에 의해 유도되는 데이터 분포는 다음과 같음

  

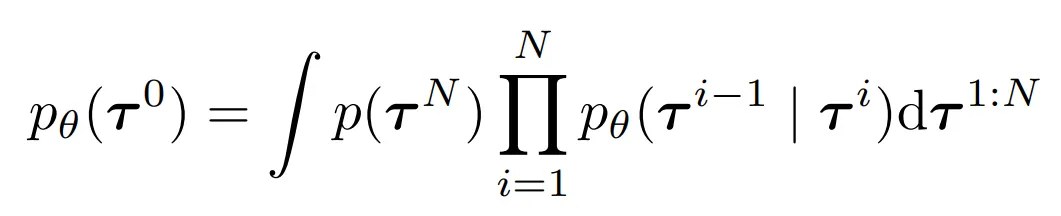
• $p(\tau^N)$: standard Gaussian prior
• $\tau^0$: noiseless data
• 파라미터 $\theta$는 reverse process의 negative log likelihood의 variational bound를 최소화하여 최적화:
  
  

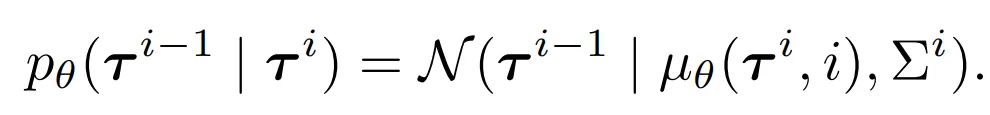
• Notation
  • 본 논문에서는 “times”라는 표현이 2가지로 사용: diffusion process, planing problem
    • superscripts는 diffusion time step을 나타냄
    • subscripts는 planning time step을 나타냄

3. Planning with Diffusion

• Trajectory optimization 기법의 주요한 장애물 → 환경 dynamics $f$에 대한 지식을 요구하는 것!
  • 대부분의 학습 기반 기법들은 이 문제를 approximate dynamics model을 학습하고 이를 기존의 planning routine에 결합
  • 그러나 학습된 모델은 ground-truth 모델로 디자인된 planning 알고리즘의 타입과는 잘 맞지 않음 → adversarial examples를 찾음
• 본 논문은 modeling과 planning을 더 강하게 결합
  • Planning 과정을 생성 모델 프레임워크에 포괄시킴 → planning과 sampling이 거의 동일하도록 함
  • 본 논문은 trajectory의 diffusion model $p_{\theta}(\tau)$를 사용
  • Diffusion model의 반복적인 denoising 과정은 purturbed distribution으로부터의 샘플링 방법을 통해 유연한 conditioning에 적합 :

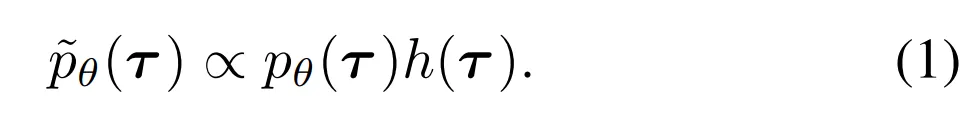
• $h(\tau)$는 다음의 정보들을 포함
  • prior evidence (ex. observation history)
  • desired outcomes (ex. goal)
  • general function to optimize (ex. rewards or costs)

• Perturbed distribution에서의 inference를 수행 → $p_\theta(\tau)$ 하에서 물리적으로 가능하며 $h(\tau)$하에서 높은 보상을 받는 (혹은 제약조건들을 만족하는) 경로들을 찾는 것을 요구함
• Dynamics 정보는 perturbation distribution $h(\tau)$와 분리되어있으므로 단일 diffusion model $p_{\theta}(\tau)$는 동일한 환경의 다른 task들에서 재활용 될 수 있음

3.1. A Generative Model for Trajectory Planning

Temporal ordering

• Trajectory model로부터의 sampling과 plannning을 모호하게 함으로써 일반적이지 않은 제약조건을 만들어냄
  • 시간에 대해 autoregressively 하게 예측을 수행하지 않고 모든 timestep에 대해 동시에 예측

Temporal locality

• Autoregressive하거나 Markovian하지 않으므로 Diffuser는 temporal locality의 특성을 보임
• Figure 2에서 single temporal convolution으로 구성된 diffusion model의 dependency graph를 묘사
• 주어진 예측의 receptive field는 오직 과거와 미래 모두에 대한 주변의 time step으로 구성
• 결과적으로 denoising 과정의 각 스텝은 경로의 local consistency에 기반하여 예측을 수행
• 이런 많은 denoising 스텝들을 함께 구성 → local consistency가 global coherence를 이끌어낼 수 있음

Trajectory representation

• Diffuser는 planning을 위해 설계된 trajectory 모델 → 즉 모델에서 파생된 컨트롤러의 효율성은 상태예측의 품질만큼 중요
  • 결과적으로 trajectory의 상태와 행동들은 함께 예측됨
  • 구체적으로 Diffuser의 입력 (그리고 출력)은 two-dimensional array로 표현

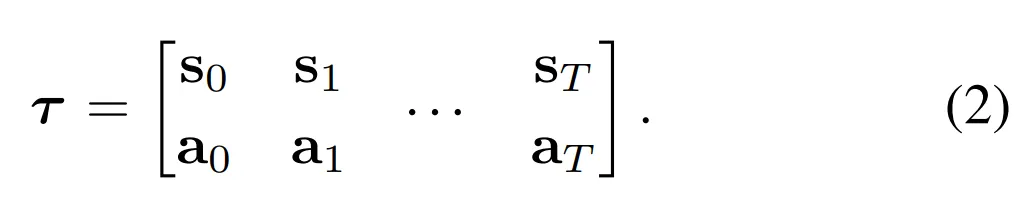
Architecture

• Diffuser 구조를 정의하기 위해 필요한 재료들
  • 전체 경로는 autoregressive하지 않게 예측되어야 함
  • Denoising process의 각 스텝은 temporally local 해야함
  • Trajectory 표현은 하나의 차원 (planning horizon)에 대해서는 equivariance 해야하지만 다른 차원 (state and action features)에 대해서는 허용되지 않아야 함
• 이런 조건들을 만족하기 위해서 반복되는 (temporal) convolutional residual blocks로 구성된 모델 사용
  • 전체적인 구조는 U-Nets의 종류를 닮음 → 이미지 기반의 diffusion model에서 사용된 모델
  • 하지만 2차원의 spatial convolution을 1차원의 temporal convolution으로 대체 (Figure A1)
  • 모델이 fully convolutional하기 때문에 예측의 horizon은 모델의 구조가 아니라 입력의 차원에 의해서 결정 → 이 때문에 planning 과정 중에 동적으로 변경하는 것이 가능함

Training

• Trajectory denoising process의 학습된 gradient $\epsilon_\theta (\tau^i , i)$의 parameterize를 위해 Diffuser 사용→ 평균 $\mu_\theta$는 closed form으로 풀릴 수 있음
• 본 논문은 $\epsilon$ 모델의 학습을 위해 단순화된 objective 사용

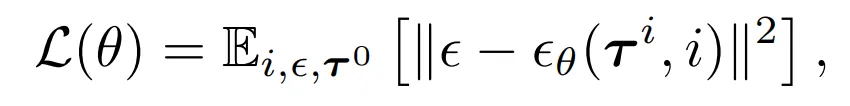
• $i \sim u\{1, 2, ..., N\}$: diffusion timestep
• $\epsilon \sim N(0,I)$: noise target
• $\tau^i$: noise $\epsilon$에 의해 손상된 trajectory $\tau^0$
• Reserve process covariance $\Sigma^i$는 Nichol & Dhariwal (2021)의 cosine schedule을 따름

3.2. Reinforcement Learning as Guided Sampling

• Diffuser를 통해 강화학습 문제를 풀기 위해서 본 논문에서는 보상의 개념을 소개
• $O_t$는 binary random variable → Trajectory의 timestep t의 optimality를 나타냄
  • $p(O_t=1)=\exp (r(s_t, a_t))$
• 이를 통해 다음과 같이 식 1의 $h(\tau)=p(O_{1:T}|\tau)$로 세팅하여 optimal trajectories의 세트로부터 샘플링 가능

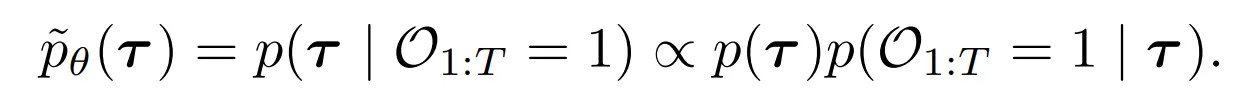
• 본 논문은 강화학습 문제를 conditional sampling 의 하나로 바꿈 → 다행히 diffusion model의 conditional sampling에 대한 이전의 연구들이 많음
• $p(O_{1:T}|\tau^i)$가 충분히 smooth할 때 reserve diffusion process transition은 Gaussian으로 근사될 수 있음

 

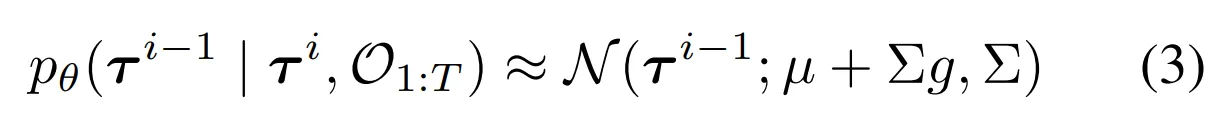
• $\mu, \Sigma$는 원래의 reserve process transition $p_{\theta}(\tau^{i-1}|\tau^i)$의 파라미터이고

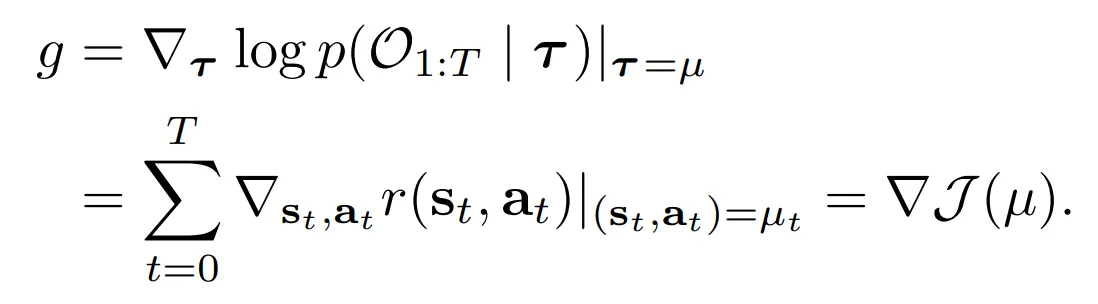
• 이 관계는 class conditional images를 생성하는 classifier-guided sampling과 강화학습 문제 세팅 사이의 직접적인 해석을 제공
  • 본 논문은 먼저 모든 가능한 경로 데이터의 상태와 행동에 대해 diffusion model $p_{\theta}(\tau)$를 학습
  • 그리고 trajectory samples $\tau^i$의 누적 보상을 예측하는 분리된 모델 $J_{\phi}$를 학습
  • $J_{\phi}$의 gradient는 trajectory sampling 과정을 가이드하는데 사용 → Equation 3의 reserve process의 mean $\mu$를 변경
  • Sampled trajectory $\tau \sim p(\tau | O_{1:T}=1)$의 첫번째 행동이 환경에서 실행될 수 있음, 이후 planning 과정은 standard receding-horizon control loop에서 다시 시작

• Guided planning 기법의 Pseudocode는 Algorithm 1에서 살펴볼 수 있음

3.3. Goal Conditioned RL as Inpainting

• 몇몇의 planning 문제들은 보상 최대화보다 제약조건들을 만족하는 것이 더 중요할 때가 있음
• 이런 세팅에서 objective는 목표 지점에서 종료되면서 제약조건들을 만족하는 feasible한 경로를 생성하는 것
• Equation 2에서 설명된 경로의 2차원 array 표현에 의해 이 세팅은 inpainting problem으로 해석될 수 있음 → 상태와 행동은 이미지에서 관측된 픽셀들 (Nichol & Dhariwal (2021))처럼 act를 제한
• Array에서 모든 관측되지 않은 정보들은 diffusion model에 의해서 반드시 채워져야함 → 관찰된 제약조건과 일치하는 방식으로
• 본 task에서 요구되는 perturbation function은 관측된 값에 대해서는 Dirac delta이며 이외에는 상수 → 자세히는 $c_t$는 시간 스텝 t에서 state constraint

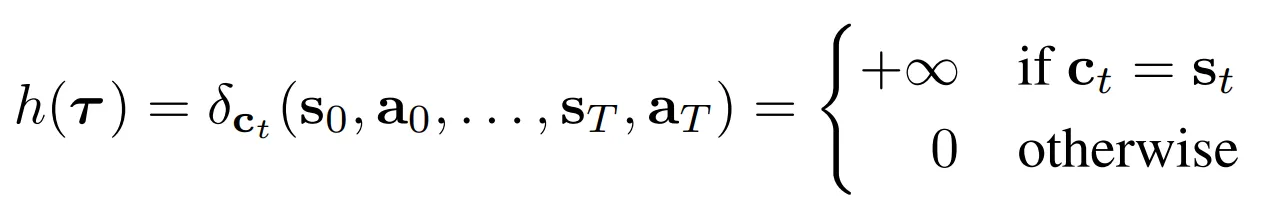
• Action constraints의 정의도 동일
• 실제로 이는 unperturbated reverse process $\tau^{i-1} \sim p_{\theta}(\tau^{i-1}|\tau^i)$로부터의 샘플링과 모든 diffusion timesteps $i \in \{0,1,...,N\}$ 이후에 sampled value를 conditioning value $c_t$로 대체하여 구현될 수 있음
• 보상 최대화 문제도 conditioning-by-inpainting을 요구 → 왜냐하면 모든 sampled trajectories는 현재 상태에서 시작해야 하기 때문 → 이 조건은 Algorithm 1의 10번째 줄에서 설명됨

4. Properties of Diffusion Planners

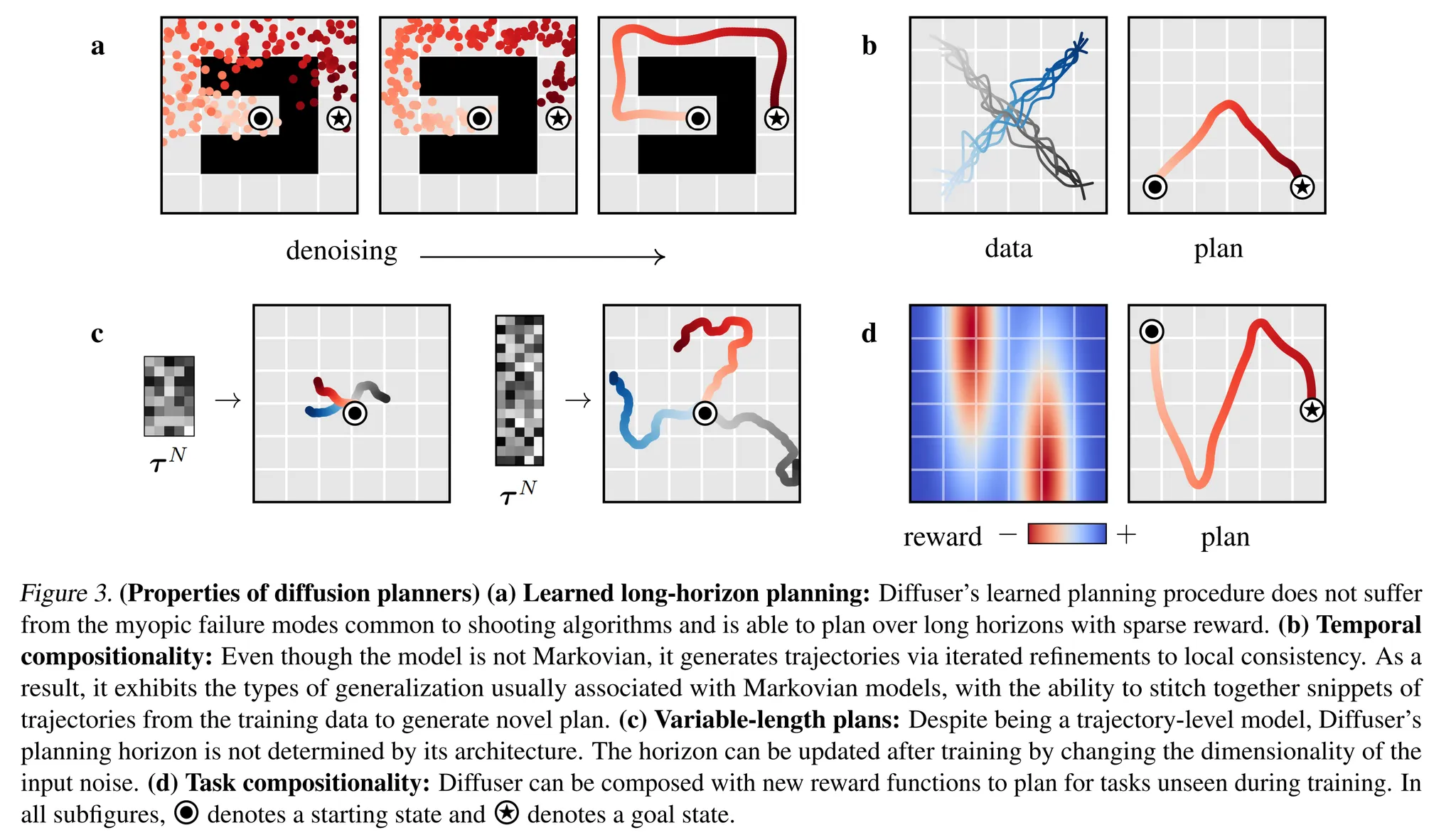
• Diffuser의 다양한 특징에 대해 논의

Learned long-horizon Planning

• Single-step model은 일반적으로 ground-truth environment dynamics $f$를 근사하기 위해 사용 → 이는 특정 planning 알고리즘과 연결되지 않음
• 대조적으로, Algorithm 1의 planning routine은 diffusion model과 밀접하게 연결
• 본 논문의 planning 기법이 sampling과 거의 유사하기 때문에 (차이는 perturbation function $h(\tau)$에 의한 guidance) Diffuser의 long-horizon predictor의 효율성이 직접적으로 효과적인 long-horizon planning으로 대응됨
• Figure 3a를 보면 Diffuser는 shooting based 접근이 어려워한다고 알려진 sparse reward setting에서도 feasible한 경로를 만들어낼 수 있음을 보임

Temporal compositionality

• Single-step 모델은 주로 Markov 특성을 사용
• Diffuser는 반복적으로 local consistency를 개선하여 globally coherent trajectories를 생성할 수 있기 때문에 이는 새로운 길의 익숙한 subsequences를 조합할 수 있음
• Figure 3b를 보면 오직 직진의 경로들로만 Diffuser를 학습하였는데 이것이 v 모양의 경로로 일반화되어 적용되는 것을 보여줌

Variable-length plans

• 본 논문은 예측의 horizon dimension에 대해 fully convolutional 구조를 가지므로 planning horizon은 구조적인 결정에 의해 구체화되는 것이 아니라 denoising 과정의 초기화 시 input noise $\tau^N \sim N(0,I)$의 크기에 의해 결정 → 다양한 길이의 planning 가능 (Figure 3c)

Task compositionality

• Diffuser는 환경의 dynamics와 행동에 대한 정보들을 포함하는 반면, 보상 함수에 대해서는 독립적임
• 모델이 가능한 미래의 prior로써 행동하기 때문에, planning은 다른 보상들에 대응하는 perturbation functions $h(\tau)$에 의해 guided (혹은 다수의 perturbations의 조합)
• Diffusion model이 학습 동안 본적 없는 새로운 보상 함수를 위한 planning의 결과 → Figure 3d

5. Experimental Evaluation

• 본 논문에서 Diffuser를 평가하기 위해 수행한 실험
  • Manual reward shaping 없이 긴 horizon에 대한 planning이 가능한지
  • 학습 동안 본적 없는 새로운 목표에 대해서도 잘 일반화 되는지
  • 다양한 quality를 가지는 heterogeneous data로부터 효과적으로 controller를 회복할 수 있는지

5.1. Long Horizon Multi-Task Planning

 

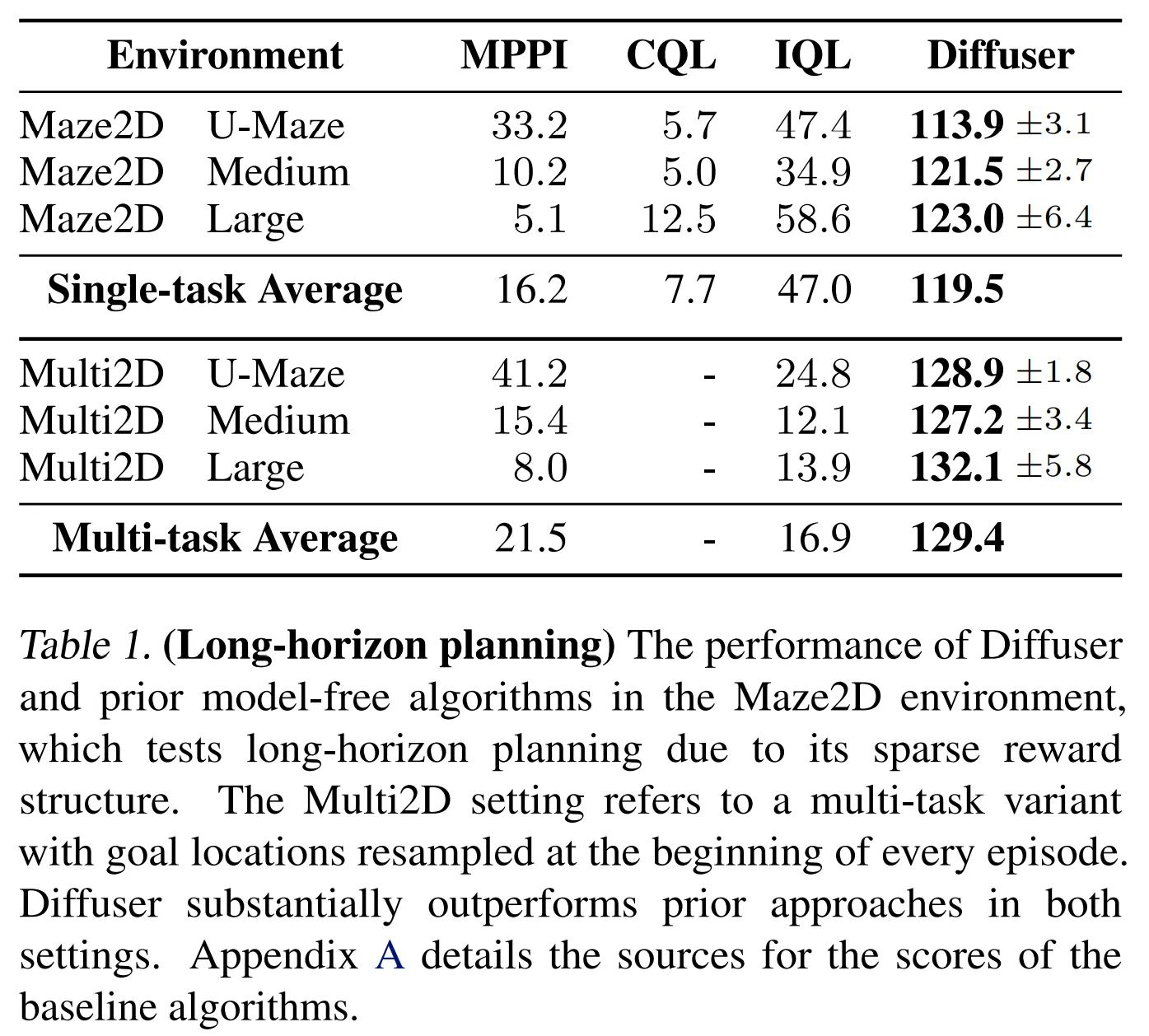
• Maze2D 환경에서 long-horizon planning 검증
  • 골에 도착하는 경우에 1의 보상 제공
  • 다른 위치에서는 reward shaping 제공 없음
  • 골에 도달하기까지 몇백 스텝이 걸림 → long horizon
• 뛰어난 model-free 알고리즘도 골에 도착하는 것에 대해 적절한 성능을 보이는 것을 어려워함 → Table 1
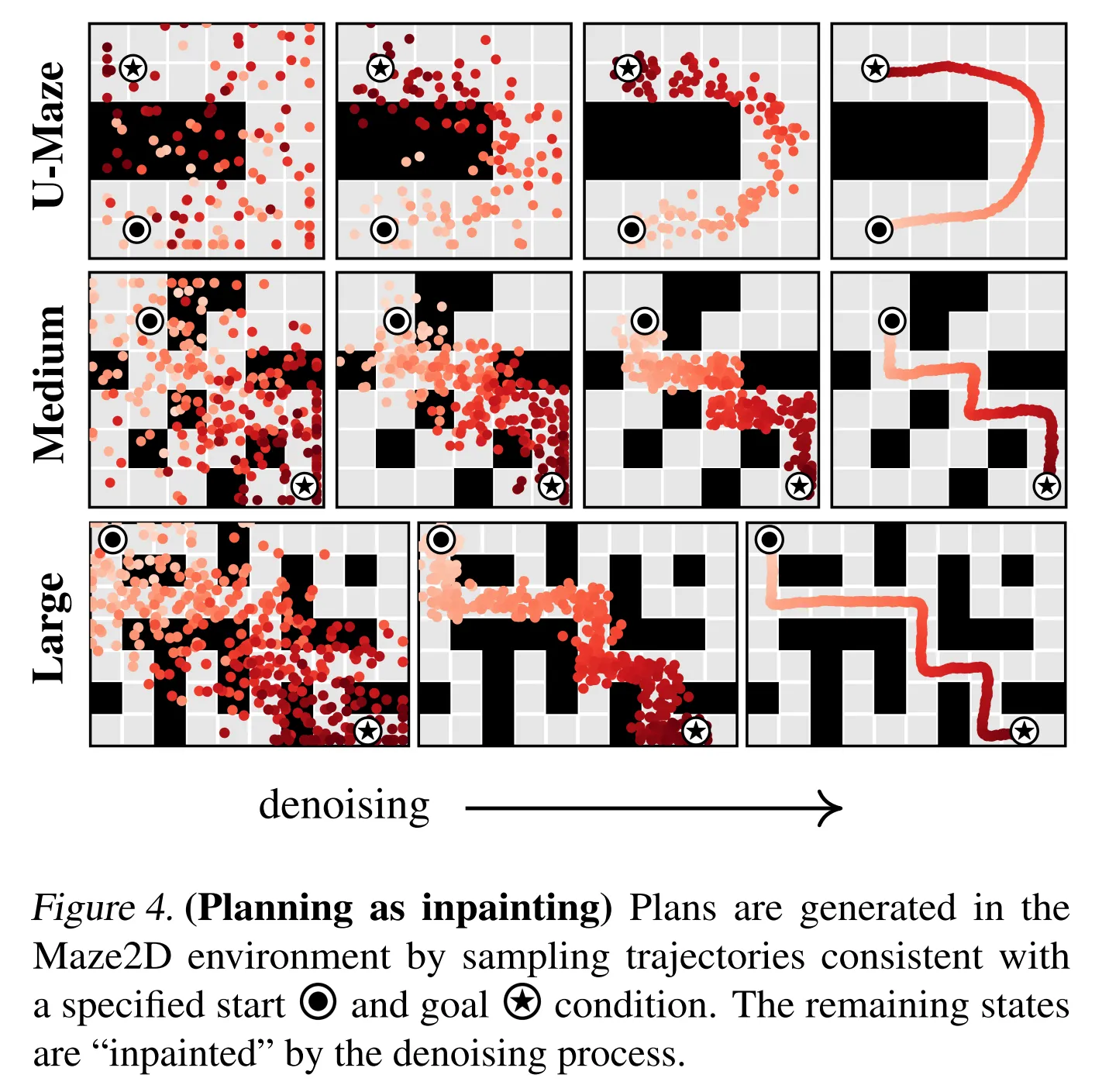
• Diffuser를 통한 planning은 시작과 골 위치에 조건을 주는 inpainting 전략을 사용
  • 그리고 sampled trajectory를 open-loop plan으로 사용
• Diffuser는 모든 미로의 크기에서 100이 넘는 점수를 달성 → reference expert policy의 성능을 능가
• Diffuser의 planning 생성의 reserve diffusion 과정을 시각화한 것 → Figure 4
• Multi-task flexibility 테스트
  • 매 에피소드마다 환경의 골 위치를 변경
  • 해당 환경은 Table 1의 Multi2D
  • Diffuser는 자연스럽게 multi-task planner의 역할을 수행 → 단순히 골에 대한 조건이 변경되는 것 때문에 모델을 재학습 할 필요 없음
  • 결과적으로 Diffuser는 single-task 세팅 뿐 아니라 multi-task 세팅에서도 좋은 성능을 보이는 것을 확인할 수 있음
  • 이와 대조적으로 single task setting에서 best model-free 알고리즘 (IQL)의 성능은 multi-task 세팅에서 감소
  • Hindsight experience relabeling을 사용한 multi-task IQL의 자세한 사용은 Appendix A에서 제공

5.2. Test-time Flexibility

 

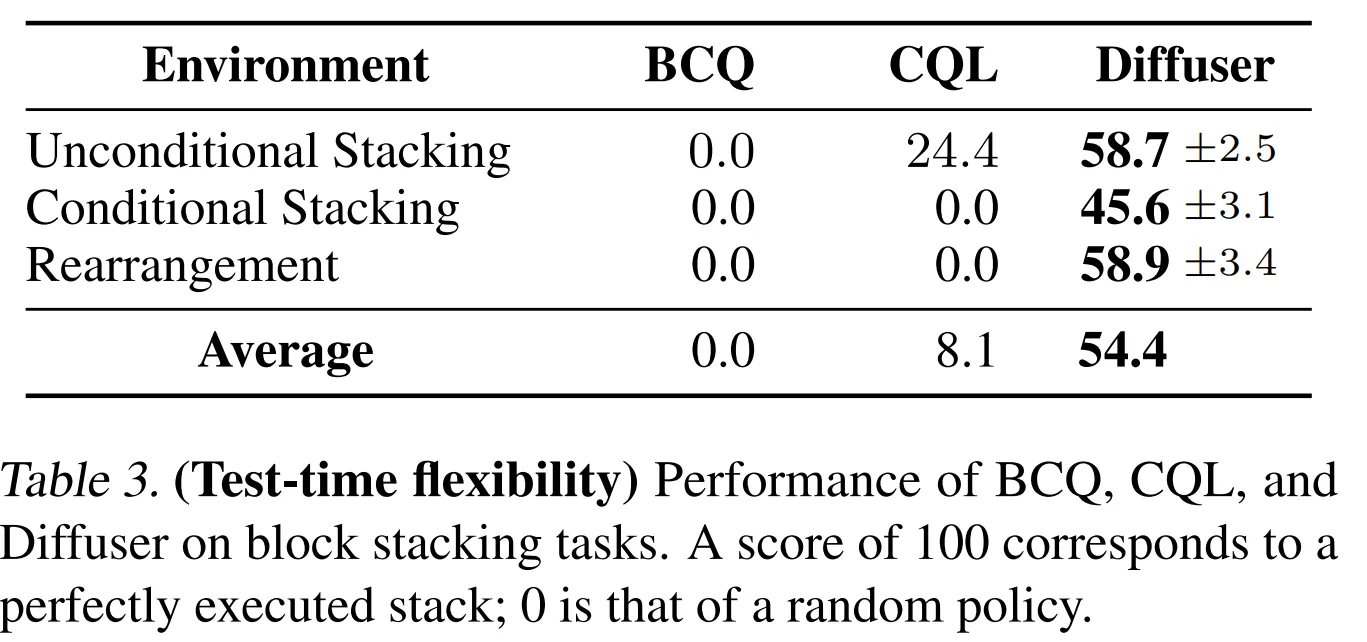
• 새로운 test-time 목표에 일반화하는 능력을 평가하기 위해 3가지 세팅을 가지는 block stacking task 사용
  • Unconditional Stacking: 가능한 높게 블럭 타워 쌓기
  • Conditional Stacking: 특정 블럭의 순서대로 블럭 타워 쌓기
  • Rearrangement: 새로운 정렬로 reference 블럭의 위치가 있으면 이와 동일하게 만드는 task
• 모든 기법을 10000 trajectory에 대해 학습하며 데모 데이터는 PDDLStream을 통해 생성
• 보상은 정확한 위치대로 쌓는 것을 성공하면 1, 그렇지 않으면 0
• 이런 블럭 쌓기는 time flexibility를 테스트하기 좋음
• 모든 블럭 쌓기 task에 대해 Diffuser 학습 → 오직 세팅간에 perturbation function $h(\tau)$만 변경
• Unconditional Stacking task → PDDLStream controller를 모방하기 위해서 unperturbated denoising process $p_{\theta}(\tau)$로부터 직접적으로 샘플링
• Conditional Stacking 그리고 Rearrangement task에서는 2개의 perterbation functions 구성
  • 첫번째는 goal configuration과 매칭되는 경로의 최종 상태의 likelihood를 최대화
  • 두번째는 stacking motion 중 end effector와 cube 사이의 contact constraint를 강제
• 두개의 model-free offline RL 알고리즘 (BCQ, CQL)과 성능 비교
  • Unconditional Stacking의 경우 표준 기법으로 학습, Conditional Stacking과 Rearrancement는 goal-conditioned variants로 학습
  • 정량적인 결과가 Table 3에 나옴 → 100점의 점수가 task를 완벽하게 끝낸 것!
  • Diffuser는 타 기법을 능가하는 성능을 보임
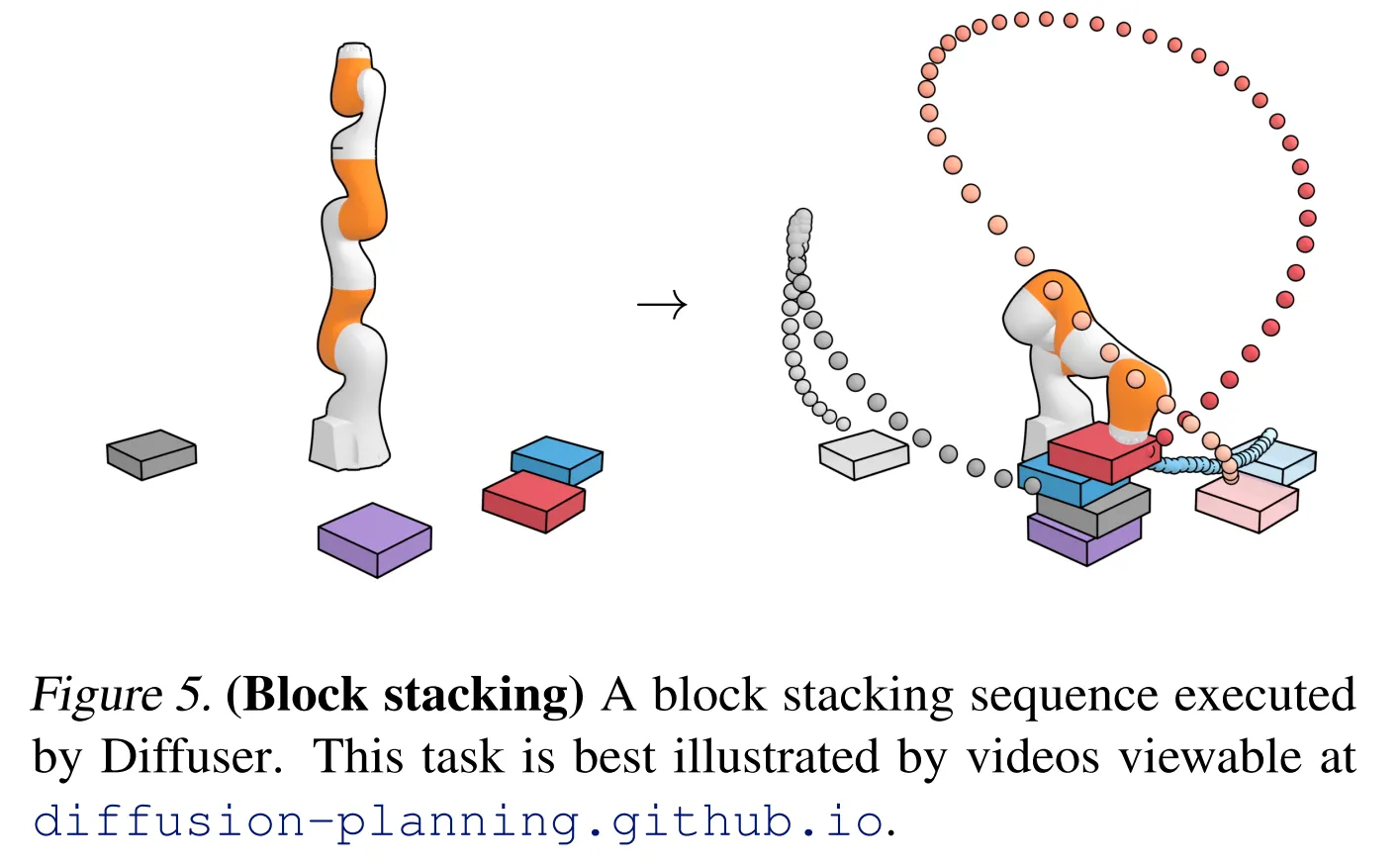
• Diffuser가 실행된 시각적인 결과는 Figure 5에서 살펴볼 수 있음

5.3. Offline RL

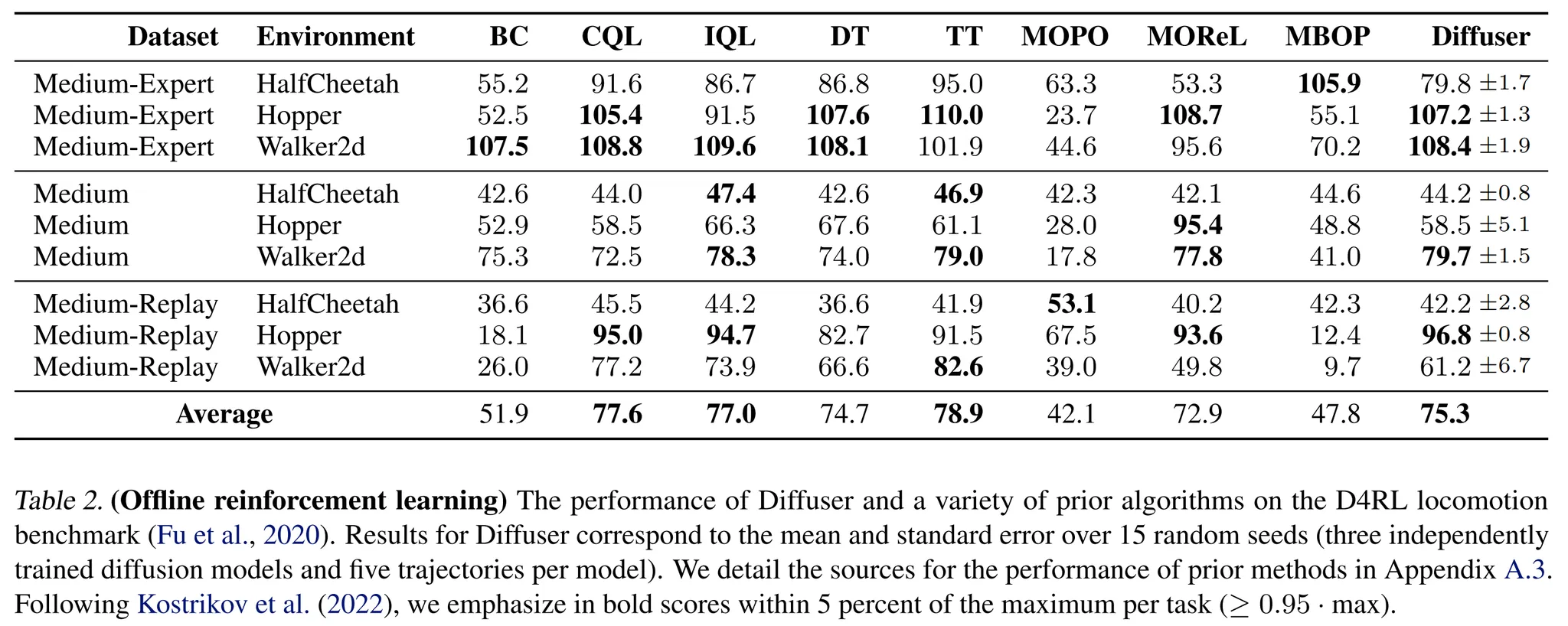
• 마지막으로 D4RL offline locomotion suite를 사용한 다양한 품질의 heterogeneous data를 통해서 효율적인 single-task controller를 회복할 수 있는지 평가
  • Diffuser에 의해 생성된 경로를 가이드 → 3.2에서 설명된 sampling 과정을 사용, 3.3에서 설명된 inpainting과정을 사용하여 현재 상태에 condition 된 경로 사용 → 높은 보상을 받도록 함
  • 다양한 model-free data-driven control 알고리즘과 성능 비교: CQL, IQL, AWAC, Decision Transformer (DT), Trajectory Transformer (TT), MOReL, MBOP
  • Single-task 세팅에서 Diffuser의 성능은 기존 알고리즘의 성능과 비교할만 함
    • MOReL, MBOP 같은 모델 기반 알고리즘에 비해 좋은 성능
    • 그러나 single task performance를 위해 구체적으로 제작된 가장 뛰어난 offline 기법에 대해서는 좋지 못한 결과를 보임

5.4. Warm-Starting Diffusion for Faster Planning

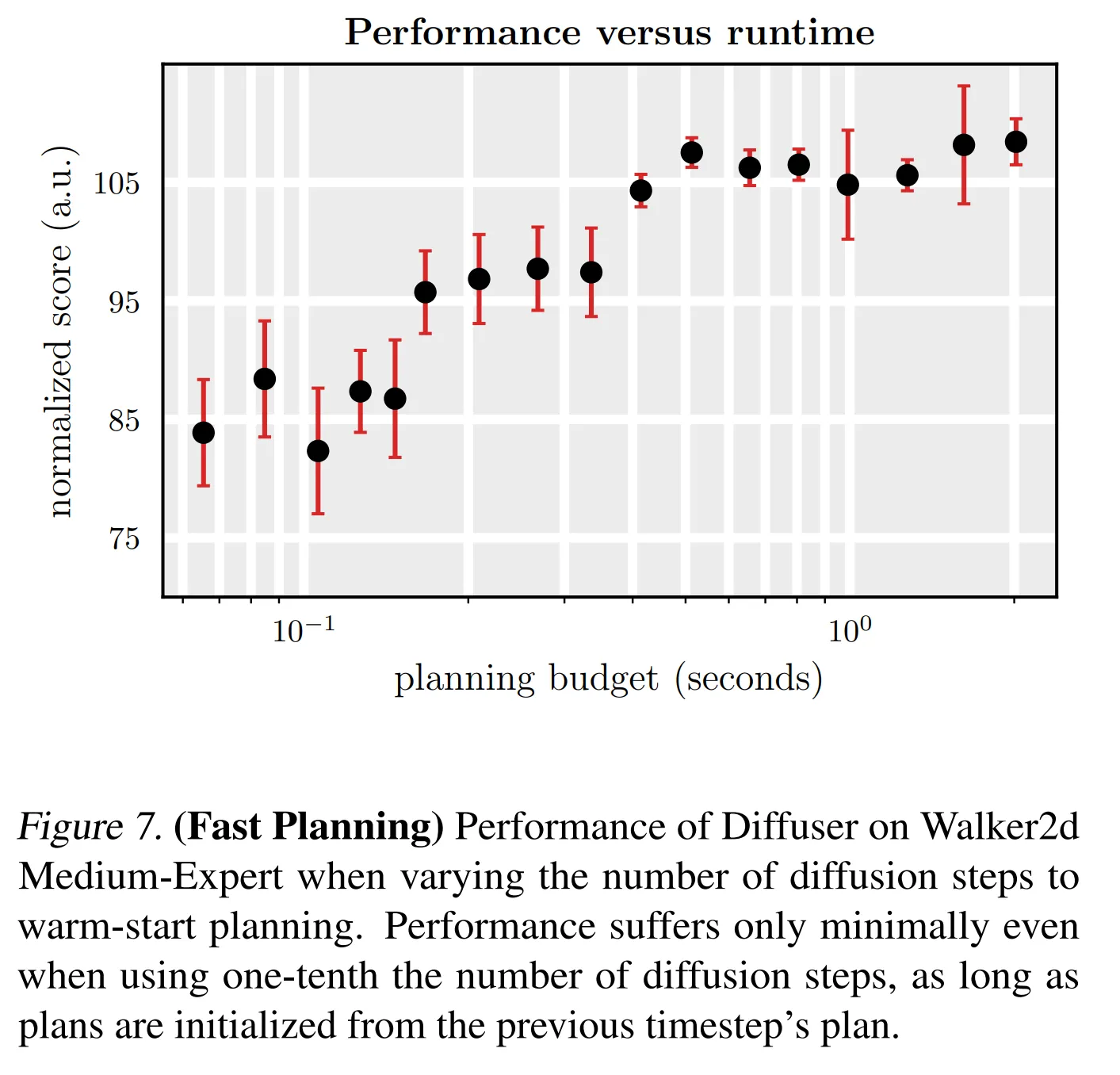
• Diffuser의 한계는 단일 planning이 반복적인 생성에 의해 천천히 수행된다는 것
  • open loop로 planning을 실행하므로 새로운 planning은 각 실행 스텝마다 재생성되어야 함
• Diffuser의 실행 속도를 향상시키기 위해서는subsequent plans의 warm start 생성을 위해 이전에 생성한 경로를 재사용 해야함
• Warm-start planning을 위해서 이전에 생성된 planning으로부터 제한된 수의 스텝만큼 forward diffusion 수행
• Figure 7에서 성능과 실행 시간 사이의 trade off를 보여줌 (새로운 planning을 재생성할 때 denoising의 수를 2-100으로 다양하게 수행)

7. Conclusion

• Diffuser → 경로 데이터를 위한 denoising diffusion model
• Diffuser를 이용한 planning은 이를 통한 샘플링과 거의 동일하지만 샘플을 가이드하는 역할을 하는 auxiliary perturbation functions가 추가되었다는 점이 다름
• 학습된 diffusion 기반 planning 과정은 몇가지 유용한 특성을 가짐
  • sparse reward에 대한 처리 가능
  • 재학습 없이 새로운 보상에 대한 planning이 가능
  • temporal compositionality → in-distribution subsequence들을 이어붙여서 out-of-distribution 경로를 만들어내는 것이 가능함
• 본 논문의 결과는 심층 강화학습을 위한 새로운 종류의 diffusion 기반 planning 과정을 보여줌