
0. Abstract
- 많은 중요한 실생활의 문제들은 높은 차원의, 혹은 연속적인 행동 공간을 가짐 → 이 모든 행동을 다 살펴보는 것은 불가능!
- 대신에 policy evaluation과 improvement를 위해 작은 행동의 subset만 샘플링하는 것은 가능
- 본 논문에서는 이렇게 샘플링 된 행동의 subset에 대해 policy evaluation과 improvement를 수행하는 general framework 제안
- 이 sample 기반 policy iteration framework는 policy iteration을 기반으로 하는 어떤 강화학습 알고리즘에도 적용될 수 있음
- 본 논문은 Sampled MuZero 알고리즘을 제안 → MuZero 알고리즘의 확장판으로 복잡한 행동 공간에서도 샘플링 된 행동을 통해 planning을 수행
- 검증은 바둑과 두개의 연속적인 제어 벤치마크 도메인 (DeepMind Control Suite, Real-World RL Suite)에서 수행
1. Introduction
- 실생활에서 많은 중요한 문제들, 대표적으로는 물리적인 제어 문제들은 연속적인 다차원의 행동 공간을 가짐
- ex. 로봇 손의 관절 각도, 자율주행차의 가속, ...
- 혹은 이산적인 행동 문제도 때때로 매우 높은 차원의 행동 공간을 가지기도 함
- 위와 같은 이유로 정말 일반적인 강화학습 알고리즘은 반드시 복잡한 행동공간을 다룰 수 있어야 성공적으로 실생활의 문제들에 적용될 수 있음
- 최근의 딥러닝과 강화학습의 발전은 다음의 영역들에서 뛰어난 발전을 보임
- 연속적인 행동 공간에 대한 model-free RL 알고리즘
- Planning 기반 기법
- 위 기법들을 결합한 알고리즘은 실생활 적용에 정말 유용할 것!
- Model-based MuZero는 강화학습 알고리즘으로 환경에 대한 모델을 학습하여 사용하므로 실생활의 문제에 적용 가능
- 장점: 환경의 dynamics를 모르거나 효과적으로 시뮬레이션할 수 없는 환경에서 planning 수행 가능
- 단점: 상대적으로 작은 행동 공간을 가지는 환경에서만 적용 가능 → tree 기반의 탐색 방법으로 모든 행동을 살펴볼 수 있어야 함
- Sample 기반 기법은 크고 복잡한 행동 공간을 다루기 위한 강력한 접근 방법을 제공
- 모든 가능한 행동에 대해 살펴보는 것이 아니라 행동들의 작은 subset을 생플링하고 해당 샘플들에 대한 최적의 policy와 value function을 계산하는 것
- 구체적으로 action sampling은 각 샘플링 된 행동의 policy를 발전시킬 수 있고 이 제안된 improvement를 평가할 수 있음
- 그러나 모든 행동 공간에 걸쳐 정책을 정확하게 발전 혹은 평가하기 위해서는 어떻게 샘플링 과정이 policy improvement, policy evalution과 상호작용하는지 이해할 필요가 있음
- 본 논문에서는 샘플링 된 행동의 작은 subset에 대해 policy improvement와 evaluation을 수행하는 프레임워크를 제안
- 어떻게 이런 local 정보가 global policy를 학습하는데 사용될 수 있는지 살펴볼 것
- planning과 local policy iteration을 위해 policy evaluation의 explicit step 수행
- 이 sample 기반의 프레임워크는 policy iteration을 사용하는 어떤 강화학습 알고리즘에도 적용 가능
- 본 논문은 Sampled MuZero를 제안 → MuZero의 확장 알고리즘으로 복잡한 행동 공간을 가지는 도메인에 적용 가능
- 이 접근법의 generality를 살펴보기 위해 2개의 연속적인 제어 벤치마크 도메인에 적용
- DeepMind Control Suite
- Real-World RL Suite
- 큰 discrete action space 환경에도 적용 → 바둑
2. Background
- 표준 강화학습은 문제를 Markov Decision Process (MDP)로 정의
- 에이전트의 행동을 정책에 의해 제어 $\pi : S \rightarrow P(A)$ ⇒ 상태를 행동 공간에 대한 확률 분포로 매핑
- 상태에 대한 반환값은 discounted future reward $G_t = \sum_i \gamma^i r(s_{t+i}, a_{t+i})$로 정의
- 에이전트의 목표는 expected return을 최대화하는 정책을 학습하는 것
- 이를 위해서 주로 사용하는 전략이 policy evaluation
- 상태 $s_t$ 혹은 상태-행동 쌍 $(s_t , a_t)$로부터 policy $\pi$에 대한 expected return 추정하는 value function을 학습
- Value function은 policy improvement라고 하는 과정에 사용될 수 있음
- 더 높은 가치를 받기 위한 개선된 정책 학습
- 이 policy evaluation, policy improvement을 반복적으로 수행하는 것이 많은 강화학습 알고리즘의 핵심! → 이를 policy iteration이라고 부름
- 이를 위해서 주로 사용하는 전략이 policy evaluation
- 이에 따라 많은 연구들이 policy evaluation과 policy improvement를 개선하는 방향에 집중
- 한가지 방향은 이미 실행된 trajectory의 정보만 사용하는 대신 현재 상태로부터 모델을 사용하여 가능한 미래의 trajectories에 대한 평가를 수행하여 효율성을 늘리는 것
- 이런 evaluation들은 해당 행동들에 대해 local하게 더 나은 정책을 만드는데 사용할 수 있음
- Monte Carlo Tree Search (MCTS)와 같은 planning 알고리즘은 local하게 더 나은 정책을 생성하기 위해 improved policy에 대한 policy evaluation의 explicit local step이 뒤따르는 policy improvement를 반복적으로 수행함으로써 다수의 local policy iteration을 수행
- 이런 관점에서 MuZero 알고리즘은 policy evaluation과 policy improvement, 두 과정이 결합된 것으로 이해할 수 있음
- Inner process → MuZero의 MCTS search 과정으로 outer process를 위한 policy improvement를 제공
- Outer process에서는 model, reward function, value function, policy 등 inner process를 위한 요소들을 학습
- Policy improvement는 parametric policy를 MuZero의 MCTS search에 의해 만들어진 개선된 정책의 방향으로 학습 → 개선된 정책 또한 행동을 하기 위해 사용
- Value function은 temporal-difference learning과 같은 policy evaluation 기법을 통해 학습
- Inner process에서 MuZero의 탐색은 다수의 analytic policy iteration step을 수행
- Policy evaluation: search tree의 values는 value function으로 bootstrapped된 평균 n-step return에 의해 explicit하게 추정됨
- Policy improvement: visits are directed toward high policy and high value action
- 이를 통해 개선된 정책과 개선된 정책의 가치 예측은 outer process에 사용될 수 있음
- 이는 몇가지 질문들을 불러옴 → action space의 적은 subset 만으로 locally improved policy를 만들기 위한 평가가 가능한가?
- 어떻게 평가할 행동이나 trajectories를 선택할 것인가?
- 어떻게 이런 행동들에 대한 locally improved policy를 만들 것인가?
- 어떻게 global policy를 학습하기 위해 locally improved policy를 사용할 것인가?
- 어떻게 이를 행동에 사용할 것인가
- 어떻게 improved policy의 policy evaluation의 explicit local step을 planning에 사용할 것인가?
- 어떻게 이런 모든 스텝들이 서로 상호작용하게 할 것인가?
- 평가될 행동들은 몇몇의 제안된 분포 $\beta$를 통해서 샘플링 됨
- 본 논문은 마지막 4개의 질문에 집중하고 샘플링 된 action subset에 대해 policy evaluation과 improvement를 수행하는 프레임워크 제안
3. Sample-based Policy Iteration
- Policy ⇒ $\pi: S \rightarrow P(A)$
- Improved policy ⇒ $I_{\pi}:S \rightarrow P(A)$는 $\pi: \forall s \in S, v^{I_{\pi}}(s) \geq v^{\pi}(s)$의 개선된 policy
- 만약 우리가 $I_{\pi}$에 완전히 접근이 가능하다면 직접적으로 이를 realisable policies의 공간에 projecting하여 policy improvement를 할 수 있음 → 그러나 action space A가 너무 크면 적은 행동의 subset에 대한 improved policy만 계산하는 것이 가능
- Locally improved policy를 통해 policy iteration을 수행하는 방법이 명확하지 않은 이유 → sampled action에 대한 정보만을 제공
3.1. Operator view of Policy Improvement
- 본 논문은 Ghosh et al., 2020에 소개된 컨셉을 사용하고 policy improvement를 두 operator의 연속적인 적용으로 분리
- (a) Policy improvement operator $I$ → 어떤 policy든 더 많은 return을 달성하는 policy로 mapping
- (b) Projection operator $P$ → realisable policies의 공간에서 이 improved policy에 대한 최선의 approximation을 찾음
- 이런 개념에 따라 policy improvement는 다음과 같이 정의 → $P \circ I$
- Ghosh et al., 2020에서 policy gradient 알고리즘은 다음과 같은 policy improvement operator를 가지는 것으로 생각할 수 있음 → $I_{\pi}(s,a) \propto \pi(s,a) Q(s,a)$ ($Q(s,a)$는 action-value function)
- 또한 PPO policy improvement operator는 다음과 같음을 보임 → $I_{\pi}(s,a) \propto \exp (Q(s,a)/\tau)$ ($\tau$는 temperatur parameter)
- 유사하게 MPO의 policy improvement operator는 다음과 같이 표기 → $I_\pi (s,a) \propto \pi(s,a) \exp(Q(s,a)/\tau)$
- AWR은 action-value function을 advantage function으로 바꾼 유사한 improved policy의 형태를 보임 → $I_\pi (s,a) \propto\pi(s,a) \exp(A(s,a)/\tau)$
3.2. Action-Independent Policy Improvement Operator
- 본 논문은 policy improvement operator를 action-independent로 정의하여 다음과 같이 표기할 수 있음 → $I_{\pi}(a|s) = f(s,a,Z(s))$
- $Z(s)$는 다음과 같이 정의되는 unique state dependent normalising factor → $\forall a \in A, f(s,a,Z(s)) \geq 0 , \sum_{a\in A}f(s,a,Z(s)) = 1$ (연속적인 행동의 경우 sum이 intergral로 대체됨)
- 위에서 설명한 모든 policy improvement operators는 action-independent
- MPO의 예시
- MPO의 policy improvement operator는 다음과 같이 적을 수 있음
- $I_{\pi}(a|s) = f(s,a,Z(s)) = \pi(s,a) \exp(Q(s,a)/\tau)/Z(s)$ and $Z(s)=\sum_a \pi(s,a) \exp(Q(s,a)/\tau)$
- MPO의 policy improvement operator는 다음과 같이 적을 수 있음
3.3. Sample-Based Action-Independent Policy Improvement Operator
- $\{a_i\}$를 제안된 distribution $\beta$를 통해 샘플링 된 $K$개의 행동이라고 하고 $\hat{\beta}(a|s) = \frac{1}{K}\sum_i \delta_{a,a_i}$는 sampled actions $\{a_i \}$에서만 non-zero인 corresponding empirical distribution
- sample-based action-independent policy improvement operator를 다음과 같이 정의
- $\hat{Z}\beta (s)$는 다음과 같이 정의되는 unique state dependent normalising factor → $\forall a \in A, (\hat{\beta}/\beta)(a|s)f(s,a,\hat{Z}{\beta}(s)) \geq 0$ and $\sum_{a \in A} (\hat{\beta}/\beta)(a|s)f(s,a,\hat{Z}_{\beta}(s))=1$
- 여기서 $(\hat{\beta}/\beta)(a|s)$는 $\hat{\beta}(a|s)/\beta(a|s)$를 단순하게 표현한 것
- $\hat{I}{\beta}\pi(a|s) = (\hat{\beta}/\beta)(a|s)f(s,a,\hat{Z}{\beta}(s))$
- MPO example
- MPO의 sample-based action-independent policy improvement operator ($\beta=\pi$ 사용)
- $\hat{I}{\beta}\pi(a|s) = \hat{\beta}(a|s) \exp(Q(s,a)/\tau)/\hat{Z}{\beta}(s)$ with $\hat{Z}\beta(s)=\sum{a}\exp(Q(s,a)/\tau)$
- MPO의 sample-based action-independent policy improvement operator ($\beta=\pi$ 사용)
3.4. Computing an expectation with respect to $I_{\pi}$
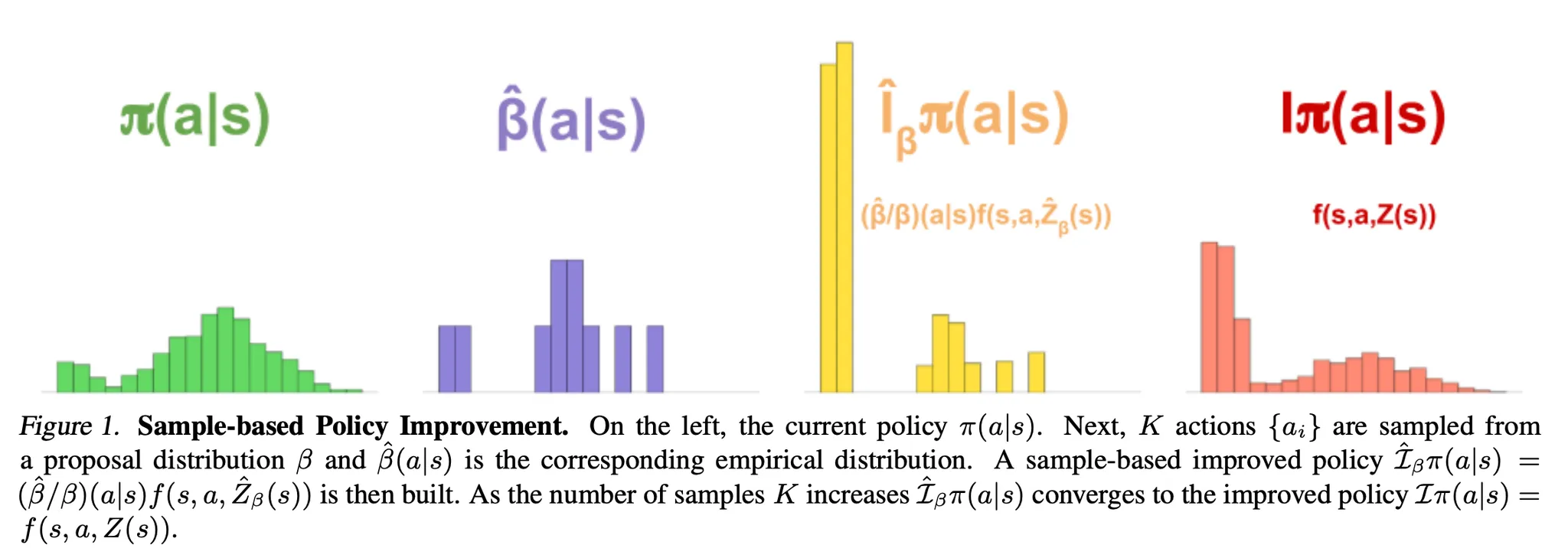
- 이번 섹션에서는 주어진 상태 $s$에 대해 distribution $\beta$와 sample based improved policy $\hat{I}\beta \pi$로 부터 샘플링 된 행동 $\{a_i \}$가 주어졌을 때 random variable $X$의 expectation $E{a \sim I_{\pi}}[X|s]$에 집중
- Theorem

-
- Sample-based policy improvement가 true policy improvement로 수렴
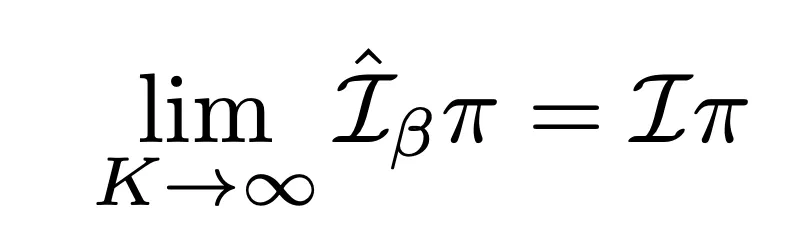
- $K \rightarrow \infty$ 이면 true policy improvement operator로 approximately normally distributed
- 위와 같은 내용을 Figure 1에서 보여주고 있음
3.5. Sample-based Policy Evaluation and Improvement
- 이전의 $E_{a \sim I_{\pi}} [X|s]$를 계산하는 수식들은 quantity $\hat{I}_{\beta}\pi$와 sampled actions $\{a_i \}$를 사용하여 계산 수행 → improved policy의 policy improvement와 policy evaluation을 위해 사용할 수 있음
- Policy improvement는 예를 들어 $X=-\log\pi_{\theta}$라 했을 때 $\pi_{\theta}$와 improved policy $I_{\pi} : CE=E_{a\sim I_{\pi}}[-\log \pi_{\theta}]$ 사이의 cross-entropy를 최소화하도록 학습
- 추가적으로 $I_{\pi}$로부터의 샘플들은 $\hat{I}_{\beta}\pi$로부터의 행동 $a$을 resampling하여 얻어질 수 있음 → 이 과정은 Sampling Importance Resampling (SIR)이라고 알려져있으며 improved policy를 통해서 행동하는 방법과 temporal-difference learning과 같은 improved policy의 policy evaluation을 할 수 있는 기법의 재사용을 가능하게 함
- 마지막으로 planning의 목적을 위해 improved policy의 policy evaluation의 explicit step은 1-step이나 n-step return으로 계산될 수 있음 → 예를 들어 $X=r+\gamma V'$이라 할 때 search tree에서 value $V'$를 다음과 같이 backpropagate할 수 있음 → $V(s) = E_{a \sim I_{\pi}}[r+\gamma V' |s]$
4. Sampled MuZero
- 이전 섹션에서 설명한 sample-based policy iteration framework를 MuZero 알고리즘에 적용 ⇒ Sampled MuZero
- MuZero가 적용될 수 있는 어떤 도메인에든 적용될 수 있을 뿐 아니라 매우 복잡한 행동 공간을 가진 모데인에서 학습 및 plan 가능
- MuZero는 policy iteration의 inner process를 MCTS로, outer process를 환경과의 상호작용으로 생각할 수 있으며 이를 결합한 기법
4.1. Inner Policy Evaluation and Improvement
- Search tree 내부에서 MuZero는 가치를 explicitly averaging n-step return samples (policy evaluation)로 추정하고 probabilistic upper confidence tree (PUCT)를 최대화하는 (policy improvement) 평가할 다음 노드를 선택한 후 확장하는 것을 반복적으로 수행

- $c(s)$는 exploration factor로 value $Q(s,a)$에 상대적인 policy $\pi(s,a)$의 영향을 조절하여 노드가 더 자주 방문되도록 함
Naive Modification
- MuZero의 MCTS 탐색을 확장하는 첫번째 방법은 sampled actions에 대해 탐색을 수행하고 PUCT 수식은 변경없이 사용하는것
- MuZero와 같이 policy network에서 나오는 확률 $\pi$를 직접적으로 사용하여 PUCT 식에 적용
- 이론적으로 이 방법은 복잡하지는 않지만 $f/\beta$ term 때문에 불안정한 결과로 이끌 수 있음 → 특히 $f$가 limited numerial precision을 가지는 normalised visit counts로 표현되는 경우
Proposed Modification
- 본 논문은 PUCT의 $\pi(s,a)$의 자리에 search probabilities로 $(\hat{\beta}/\beta \pi)(s,a)$에 비례하는 $\hat{\pi}_{\beta}(s,a)$를 제안 → 이를 통해 MuZero와 같이 visit count distributions를 도출
- Theorem
- $I_\pi$: 모든 행동 공간을 고려헀을 때 MuZero search의 visit count distribution
- $I_{\hat{\pi}{\beta}}$: prior $\hat{\pi}{\beta}$를 통한 탐색으로 얻어진 visit count distribution
- 이때 $I_{\hat{\pi}{\beta}}$는 근사적으로 $I{\pi}$와 관련된 sample-based policy improvement와 동일
- ⇒ $I_{\hat{\pi}{\beta}}\approx \hat{I}{\beta}\pi$
4.2. Outer Policy Improvement
- MCTS 내부에서 policy improvement와 policy evaluation의 inner iteration이 완료되면 net result는 search tree의 root state $s$에서 각 sampled action $a$에 대한 visit counts $N(s,a)$
- Visit count는 sample-based improved policy $I_{\hat{\pi}_\beta}(a|s)=N(s,a)/\sum_b (s,b)$를 제공하기 위해 normalised
- Visit count는 root action이 $\beta$에 따라 sampling 되었다는 것을 이미 고려
- 이제 남은것은 적절한 projection operator $P$를 이용하여 sample-based improved policy를 representable policies의 space로 project하는 것
- MuZero를 따라 확률 분포를 위한 표준 projection operator는 KL divergence $KL(I_{\hat{\pi}\beta}||\pi{\theta})$를 최소화 하는 것
4.3. Outer Policy Evaluation
- 행동을 선택하기 위해서 에이전트는 행동을 sample-based improved policy $I_{\hat{\pi}_\beta}(a|s)=N(s,a)/\sum_b N(s,b)$로부터 샘플링 → 직접적으로 policy로 사용
- Outer policy evaluation 스텝은 MuZero를 직접적으로 따름
- value function은 sample-based improved policy를 통해 생성된 행동의 trajectory를 사용하여 n-step return을 구하고 이를 통해 학습
4.4. Search Tree Node Expansion
- MuZero에서는 leaf node가 확장될 때 모든 $N=|A|$ 행동 공간의 행동이 반환되고 policy network의 확률 $\pi$가 각 행동들에 할당
Proposed Modification
- Sampled MuZero에서는 distribution $\beta$로 부터 $K \ll N$ 개의 행동을 샘플링 → 확률 $\pi(s,a)$와 $\beta(s,a)$에 따라 각 행동 $a$ 반환
4.5. Sampling distribution $\beta$
- 이론적으로는 uniform distribution을 포함해서 어떤 sampling distribution $\beta$ with wide support가 사용될 수 있음
- 하지만 적은 수의 샘플들만 뽑기 때문에 현재 추정되는 best policy (i.e. policy network)를 사용하여 샘플을 뽑는 것을 선호함
Proposed Modification
- 본 논문은 $\beta = \pi$를 사용 → temperature parameter에 의해 modulated
- 탐험을 유도하고 낮은 prior행동도 선택될 수 있도록 하기 위해서 MuZero는 policy network에 의해 도출되는 prior $\pi$에 search tree의 root node에서 Dirichlet noise를 더해줌
- Sampled MuZero에서도 동일하게 수행 → $\beta$와 $\pi$에 노이즈 추가 → 낮은 prior의 행동도 샘플링되고 탐색될 수 있도록
5. Experiments
- Sampled MuZero의 성능 평가
- 실생활의 문제 적용을 위한 2가지 중요한 특성을 살펴보기 위해서 벤치마크 사용
- Sampled MuZero가 다양한 종류의 discrete와 continuous 행동 환경에서 충분히 일반화 되는지
- 알고리즘이 샘플링에 강인한지 → 적은 수의 행동만 샘플링해서 사용할 때 모든 행동을 사용하는 것에 비해서 어느정도 가까운 성능을 보이는지!
- 실생활의 문제 적용을 위한 2가지 중요한 특성을 살펴보기 위해서 벤치마크 사용
5.1. Go
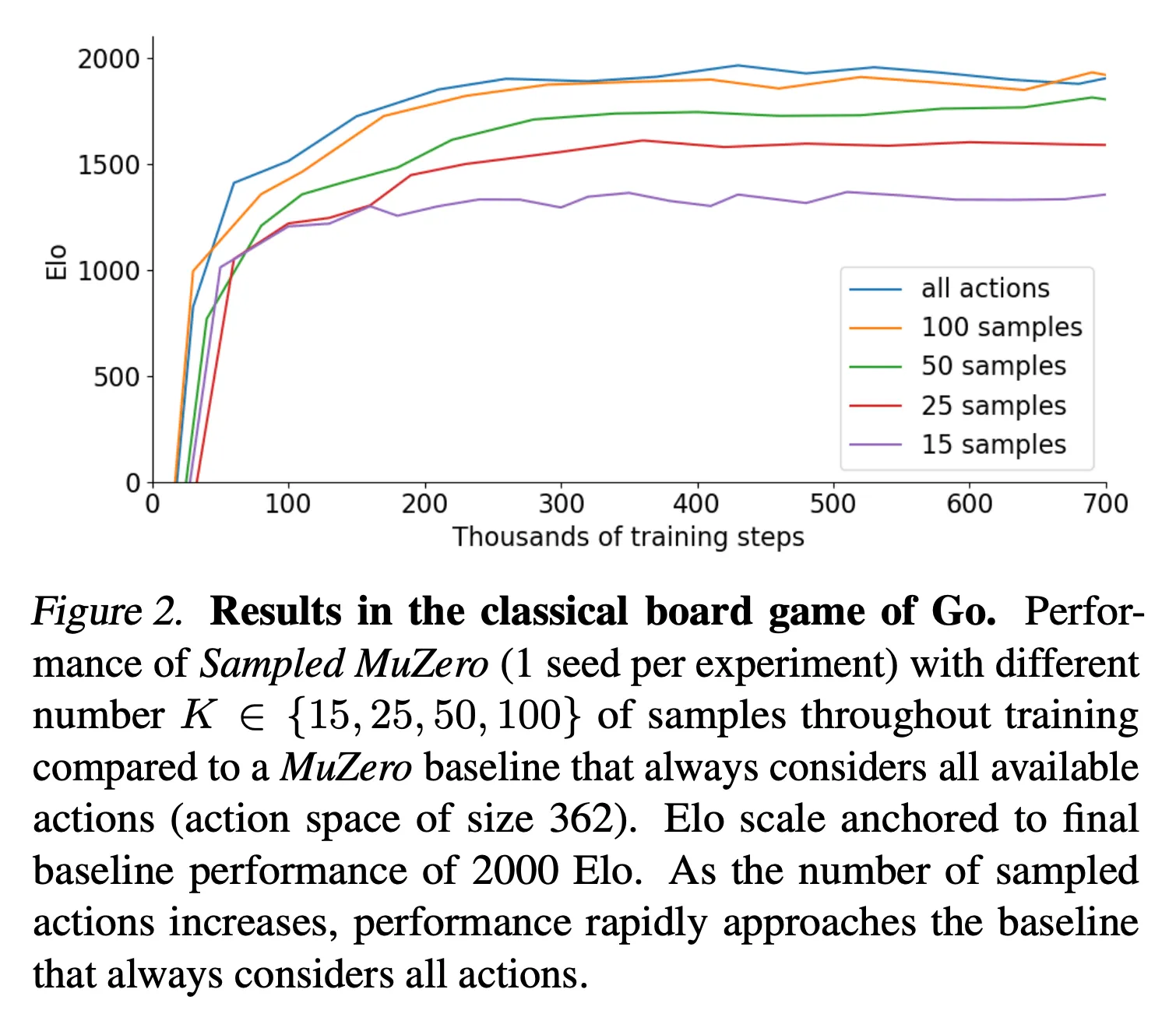
- 바둑의 경우 깊고 정확한 planning을 수행해야 하기 때문에 Sampled MuZero의 planning 성능을 확인하기 좋은 도메인
- MuZero를 베이스라인으로 하여 Sampled MuZero에서 샘플링 하는 행동의 수를 다양화하며 성능을 검증 → $K \in \{15, 25, 50, 100 \}$ (Figure 2 참고)
- $K=50$으로 해도 베이스라인의 성능과 유사
5.2. Atari
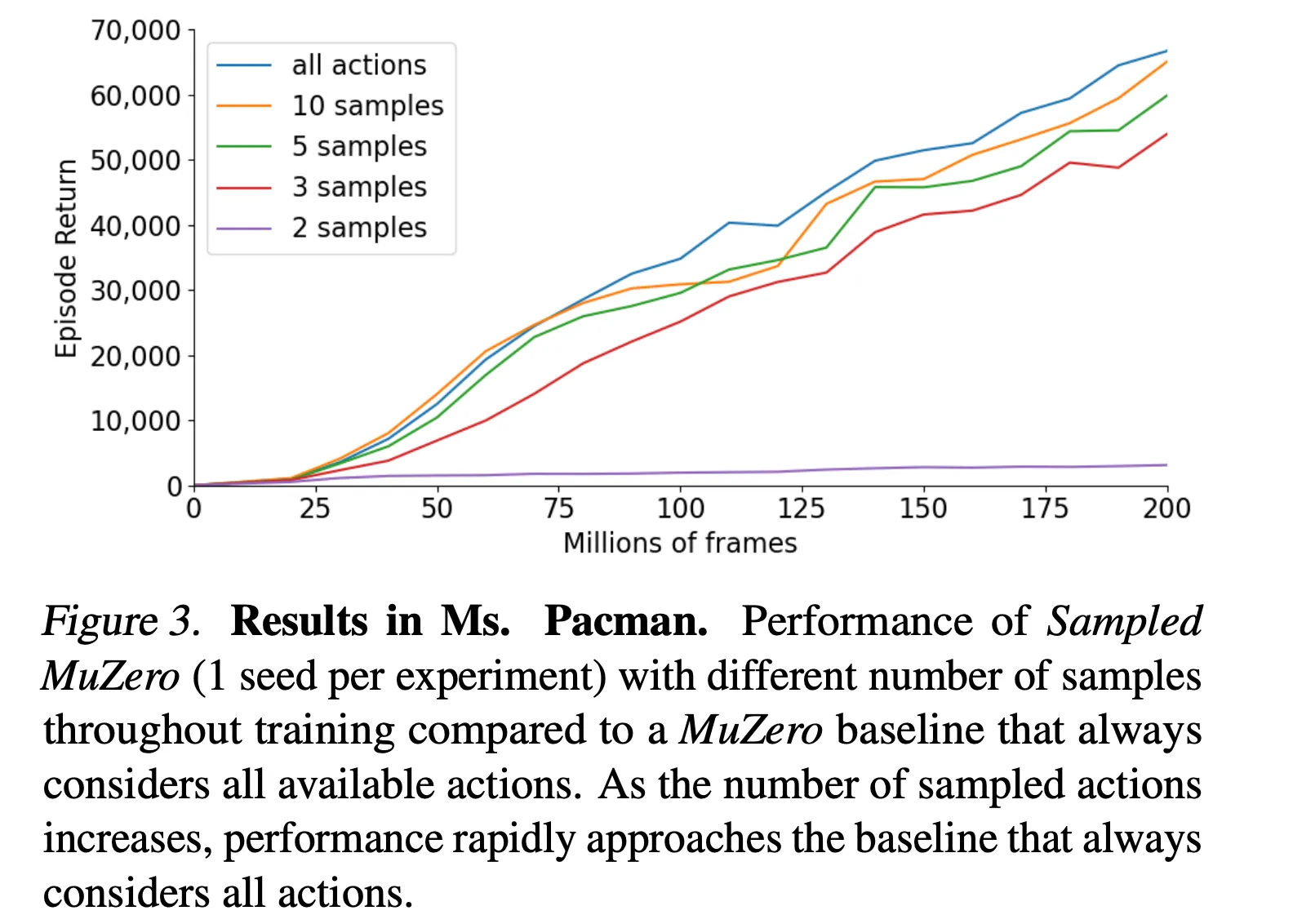
- Atari의 Ms. Pacman에서 성능 검증
- Atari의 행동 공간 크기는 18 → $K=2$인 경우는 학습에 충분치 않음
- 하지만 $K=3$부터 성능이 빠르게 증가하여 하여 베이스라인 성능에 근접
5.3. DeepMind Control Suite
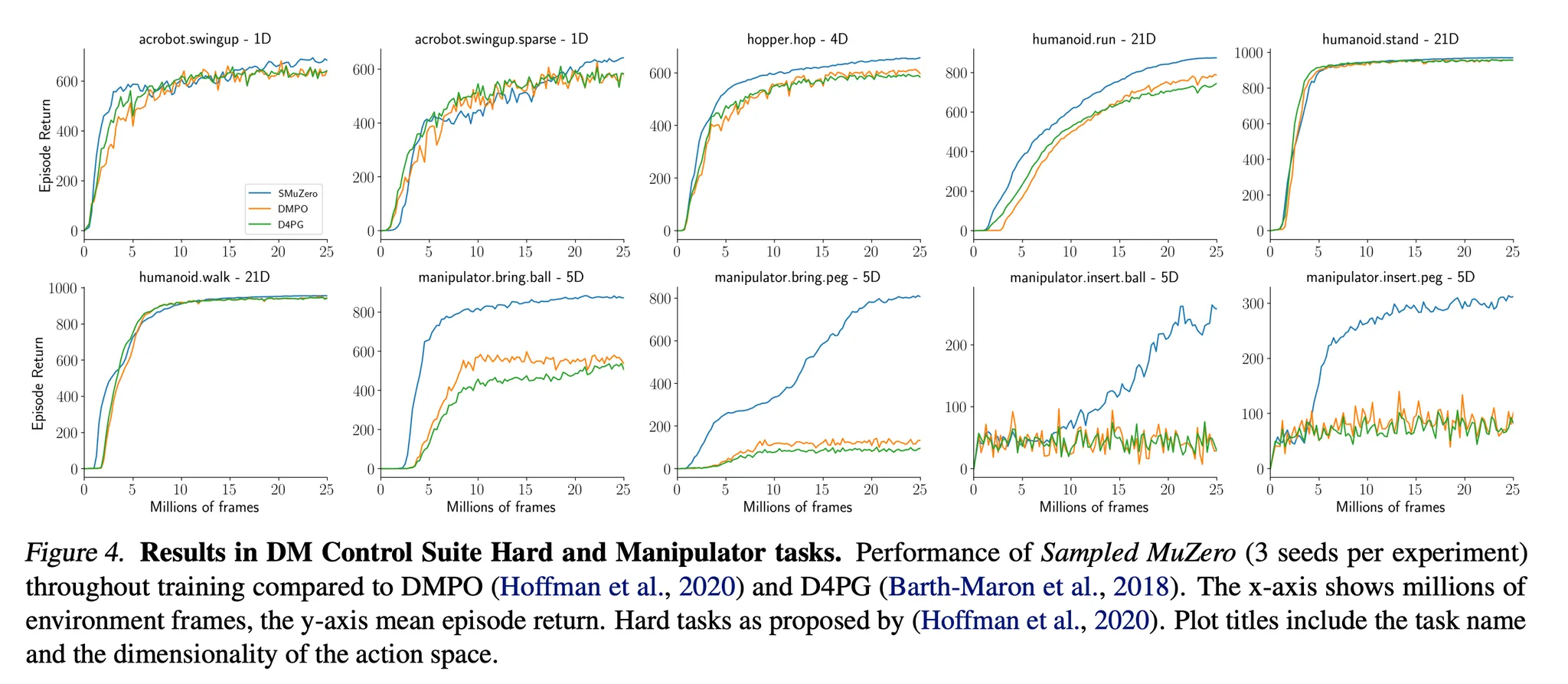
- DeepMind Control Suite는 MuJoCo에 기반하여 연속적인 행동 task들을 제공 → 연속적인 제어 알고리즘의 성능을 평가하는 벤치마크로 널리 사용됨
- Easy, medium, hard task에서 Sampled MuZero 성능 평가
- 흥미롭고 어려운 문제로 알려진 manipulation task에서도 Sampled MuZero의 성능 평가
- Control suite 도메인은 벡터 차원의 상태를 입력으로 사용
- 이에 따라 MuZero의 모든 convolution을 fully connected layers로 대체 (Appendix A 참고)
- Policy 예측에 대해서는 Tang & Agrawal, 2020에서 소개된 factored policy representation 사용
- 각 dimension을 categorical distribution으로 표현
- 하지만 continuous action의 경우 직접 작업해도 어려운 부분이 없기 때문에 hard and manipulation task에서는 policy prediction을 Gaussian distribution으로 parameterise (Figure A.1)
- Sampled MuZero는 task set에 대해서 좋은 성능을 보임 (Full result = Figure 7 참고)
- 특히 어려운 hard and manipulation 카테고리에서 좋은 성능을 보임 (Figure 4) → humanoid.run이나 manipulation task
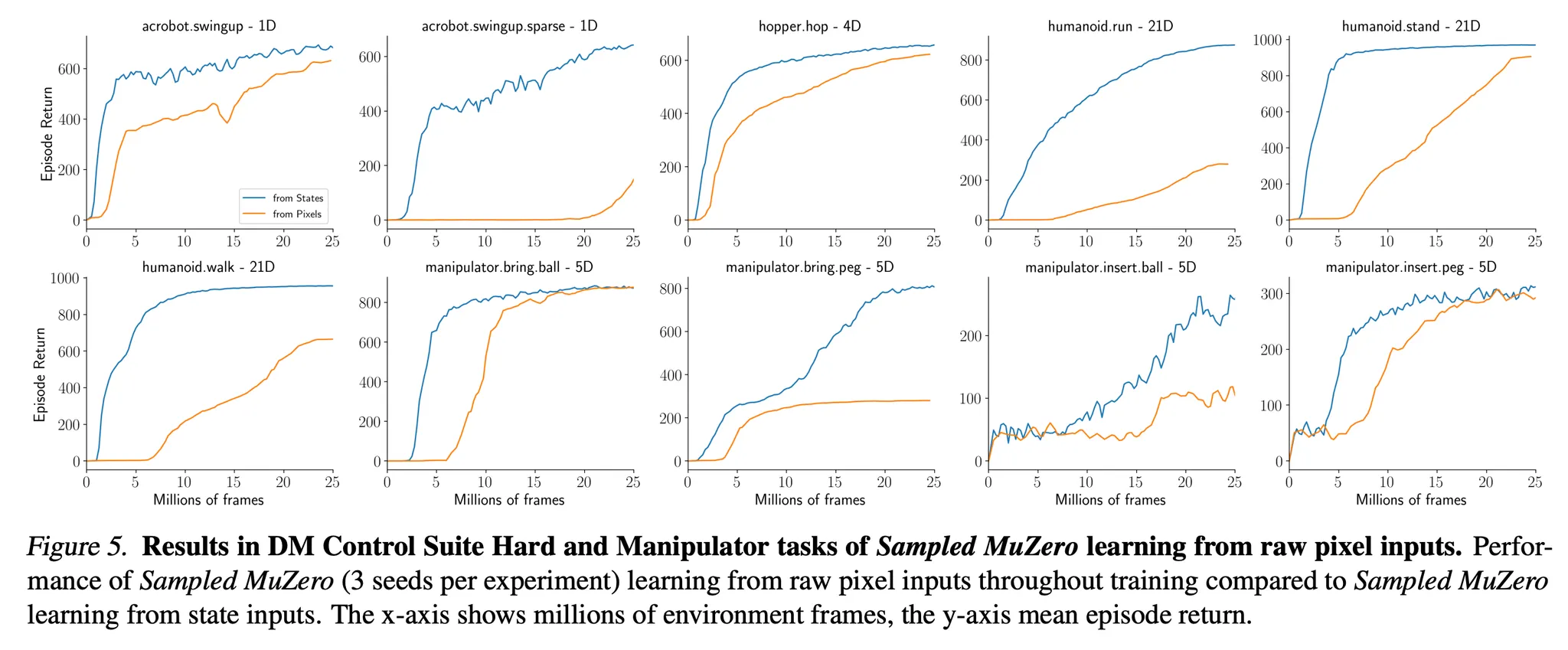
- Control suite 도메인은 벡터 상태 입력 뿐 대신에 raw pixel 입력을 제공하기도 함
- Figure 5를 보면 Sampled MuZero가 raw pixel 입력에 대해서도 효과적으로 학습하는 것을 알 수 있음 → 특히 21 차원의 행동 공간을 가지는 humanoid에 대해서 raw pixel input만으로 학습이 가능하다는 점이 인상적임!
- Sampled MuZero를 Dreamer와 성능 비교 (Appendix A.2, Table 2)
- Sampled MuZero의 경우 Dreamer 에이전트의 성능에 비해 action repeat, observation reconstruction, hyperparameter re-tuning을 사용하지 않고도 모든 task에서 유사하거나 더 나은 성능을 보임
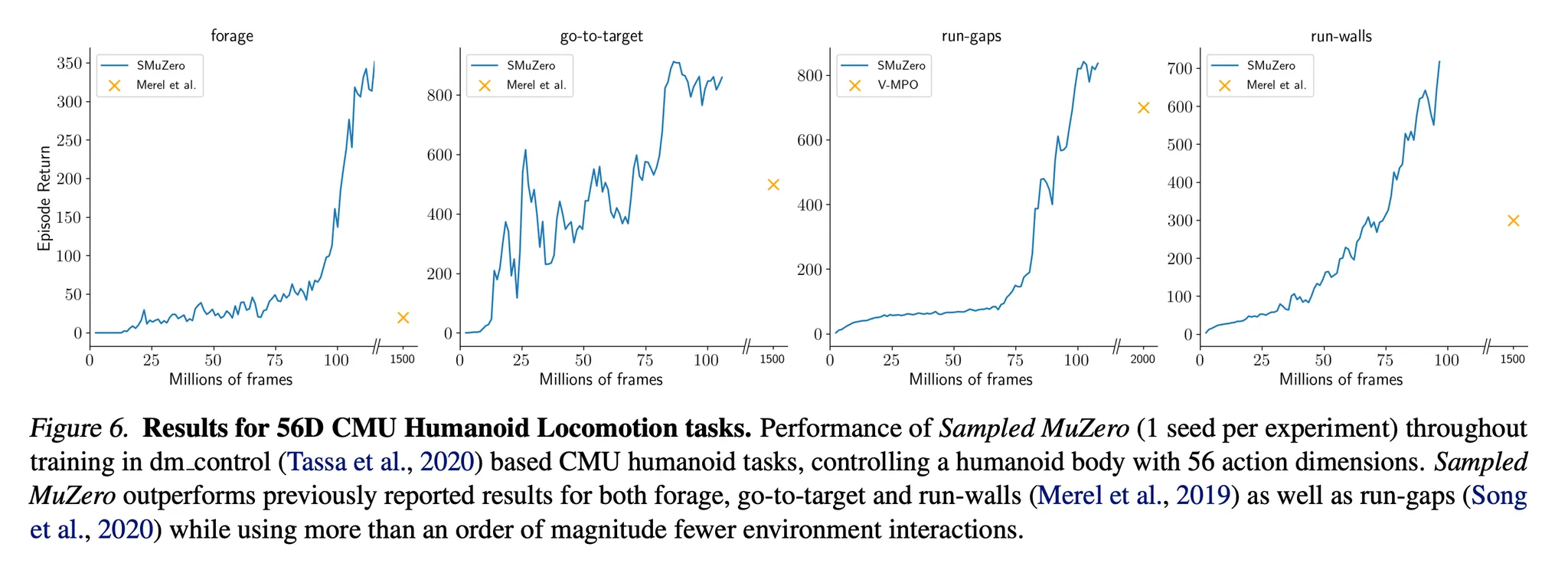
- 더 복잡한 행동 공간에 대해서도 scalability를 보기 위해서 Sampled MuZero를 Locomotion 환경을 기반으로 하는 dm_control에도 적용
- 고차원의 task → 에이전트는 56개의 행동 차원을 가지는 humanoid를 제어해서 목표를 달성해야함 (Figure 6)
- 모든 task에서 Sampled MuZero는 기존에 보고된 결과들을 능가할 뿐 아니라 환경과 더 적은 상호작용을 수행
- 마지막으로 샘플의 수가 성능에 미치는 영향에 대해 조사 (Figure 10)
- Sampled MuZero는 고차원의 행동 차원을 가지는 task에 대해서도 K=5 샘플로도 학습이 가능
- State input과 raw pixel input에 대한 성능을 Figure 11, 12에서 살펴볼 수 있음
- Figure 13에서는 Sampled MuZero의 PUCT에서 $\pi$ 대신 $\hat{\pi}_\beta$를 사용한 것의 중요도를 검증
- $\hat{\pi}_\beta$를 사용하는 것이 훨씬 robust한 성능을 보임
5.4. Real-World RL Challenge Benchmark
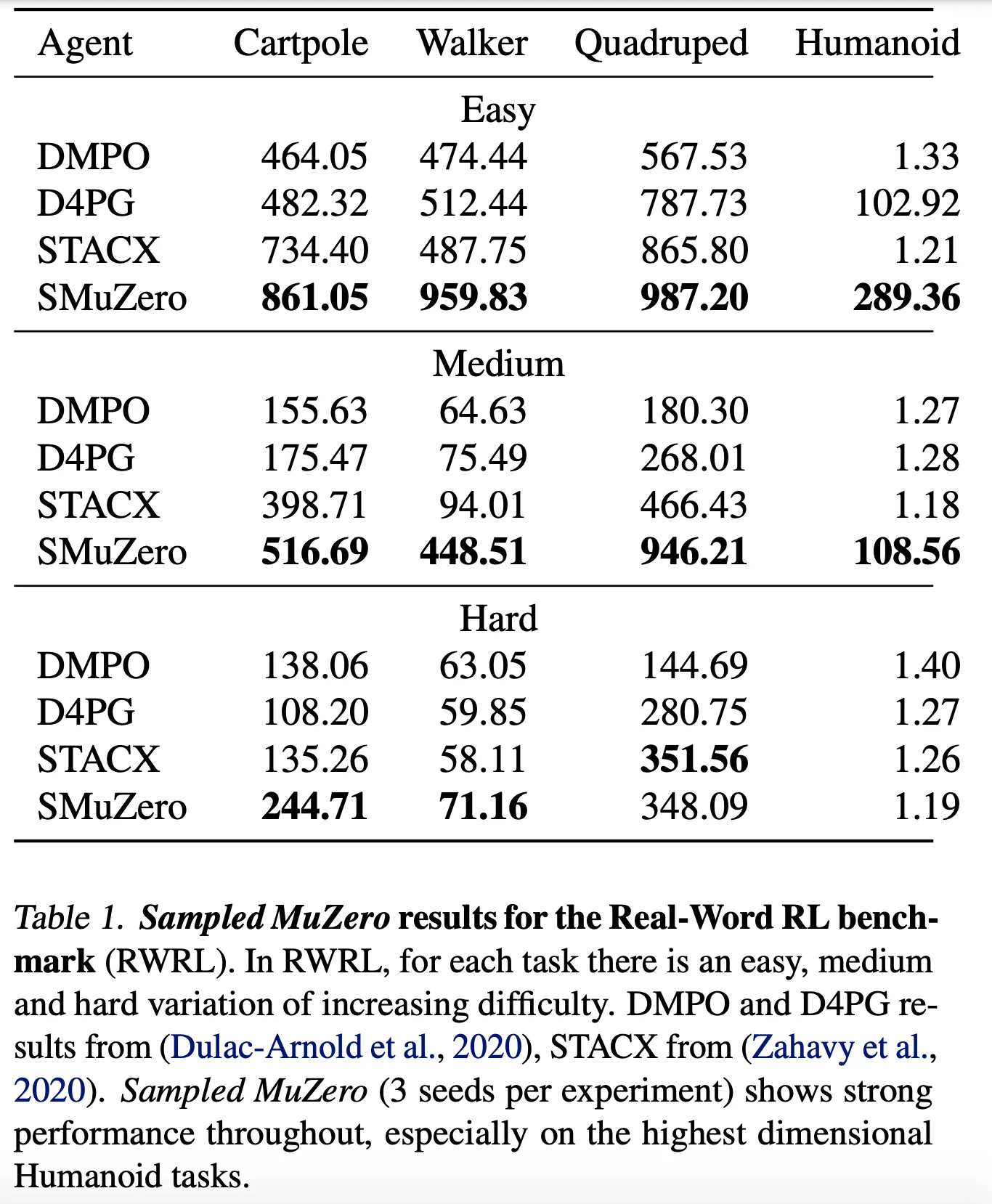
- Real-World Reinforcement Learning (RWRL) Benchmark는 일반적으로 RL이 실패하는 실생활의 continuous control task를 포함
- Delay나 partial observability, stochasity를 포함하여 robustness를 테스트할 수 있음
- DeepMind Control Suite와 동일하게 LSTM을 추가하여 partial observability에 대응하도록 함
- Table 1에서 볼 수 있듯이 Sampled MuZero는 3개의 난이도에서 타 알고리즘에 비해 뛰어난 성능을 보임
- 모든 learning curve는 Appendix의 Figure 8 참고
6. Conclusions
- 본 논문에서는 discrete, continuous 그리고 복잡한 행동 공간에서 learning과 planning이 가능한 unified framework 소개
- Sampling actions라는 단순한 원리를 적용한 접근
- 동일한 sample 기반 방법은 policy가 action-independent improvement step을 통해 업데이트 되거나 근사되는 다른 강화학습 알고리즘에도 적용 가능
- 해당 프레임워크를 model-based planning 알고리즘인 MuZero에 적용하여 새로운 알고리즘을 제시 → Sampled MuZero
- 본 논문의 empirical result
- discrete, continuous benchmark 환경에 일반적으로 적용 가능
- 적은 수의 sample로도 좋은 성능을 보여 robustness와 scaling 성능을 보임
- 이를 통해 모든 행동 공간을 살펴볼 수 없는 large scale application에 대해서도 효과적임을 보여줌
'논문 리뷰 > Reinforcement Learning' 카테고리의 다른 글
| Planning with Diffusion for Flexible Behavior Synthesis (0) | 2024.11.03 |
|---|---|
| Estimating Risk and Uncertainty in Deep Reinforcement Learning (0) | 2024.11.03 |
| [MuZero] Mastering Atari, Go Chess and Shogi by Planning with a Learned Model (2) | 2024.09.22 |
| [M-RL] Munchausen Reinforcement Learning (1) | 2024.09.16 |
| [RND] Exploration by Random Network Distillation (1) | 2024.09.13 |



