
0. Abstract
- 강화학습 에이전트는 2 종류의 uncertainty를 만나게 됨
- Epistemic Uncertainty: 데이터의 부족 때문에 발생 → exploration을 통해 해결 가능
- Aleatoric Uncertainty: 확률적인 환경에서 발생 → risk sensitive한 application에서 고려되어야 하는 부분
- 본 논문에서는 학습된 Q 값에 대해 이런 uncertainty를 분리하여 추정하는 방법론을 제안
- Uncertainty-aware DQN
- MinAtar 테스트 환경에서 다른 DQN 기반 알고리즘보다 좋은 성능을 보였으며 안전하게 행동을 취하도록 학습
1. Introduction
- 강화학습에서 환경에 있는 epistemic uncertainty와 aleatoric uncertainty를 구분하는 것은 탐험과 risk-sensitivity의 측면에서 중요함!
- Epistemic uncertainty: 제한된 데이터 때문에 발생
- Aleatoric uncertainty: 환경의 내재적인 확률성 때문에 발생
- 기존의 연구들은 두 uncertainty를 추정하는 독립적인 기법을 사용
- 예를 들어 distributional RL의 경우 평균 가치만을 구하는 것이 아니라 이에 대한 분포를 구함 → aleatoric uncertainty를 구할 수 있는 방법
- 학습된 분포의 분산은 in-distribution data에 대해서 aleatoric uncertainty를 구할 수 있는 좋은 방법이지만 out-of-distribution data, 즉 epistemic uncertainty가 높은 경우 이는 좋은 지표가 아님
- 본 논문의 기법은 다음의 기법들을 기초로 함
- Distributional RL
- Bayesian deep learning
- 본 논문의 main contributions
- Aleatoric uncertainty와 epistemic uncertainty를 분리해서 추정할 수 있는 이론적인 프레임워크 제안
- 두 종류의 uncertainty를 구하기 위한 실용적이고 unbiased estimator 제안
- 이런 uncertainty 들을 uncertainty-aware DQN 알고리즘에 성공적으로 적용
Background
- Distributional RL (참고: https://reinforcement-learning-kr.github.io/2018/10/22/QR-DQN/)
- 반환값의 분포 Zπ(s,a)를 학습하는 것이 목표
- 이를 학습하기 위해 quantile parameterization 기법 제안
- 해당 기법에서 확률 분포 Z(s,a)는 value q=(q1,...qN)을 가지는 N 개의 quantiles τi=i/(N+1)로 parameterized 됨
- 다음의 quantile regression loss를 최소화 하는 방법으로 quantile value를 학습

2. Estimating Both Uncertainties
2.1. Theoretical Framework
- Bayesian inference problem으로 return distribution의 quantile 학습
- Zπ(s,a)의 주어진 quantile τ의 가치를 학습하기 위해 파라미터 θ를 가지는 neural network 사용 → value y(θ,s,a) 반환
- 네트워크의 출력이 데이터와 매칭되는지 확인을 위해 asymmetric Laplace distribution 사용 → 이에 기반한 likelihood를 다음과 같이 정의

- 하나의 quantile이 아니라 모든 return distribution을 추정해야 하므로 위의 식을 N개의 출력 yi(θ,s,a)에 적용 → 각각의 출력 i가 quantile τi의 가치를 학습
- 이에 따라 likelihood를 다음과 같이 다시 정의

- 식 1의 loss를 최소화하는 것은 식 3의 likelihood를 최대화 하는 것과 동일
- 만약 우리가 파라미터 θ에 대해 0을 중심으로 하는 normal prior를 고려한다면 posterior distribution P(θ|D)로부터 근사적으로 샘플링을 하는 몇가지 방법 중 어떤 것도 사용 가능
2.2. Uncertainty Estimated
2.2.1. Epistemic Uncertainty
- Return distribution에 대한 epistemic uncertainty의 단일 measure를 얻기 위해 본 논문은 quantiles에 대한 epistemic uncertainty의 평균을 취함 → θ에 대한 variance로 정의

- U{1,N}은 {1,N}에 대한 uniform distribution
2.2.2. Aleatoric Uncertainty
- Aleatoric uncertainty의 직관적인 지표는 quantile 값에 대한 분산
- 그러나 이 분산은 θ에 대한 분포의 형태로 epistemic uncertainty에 의해서 영향을 받음
- Aleatoric uncertainty를 epistemic uncertainty로부터 분리하기 위해서 aleatoric uncertainty를 θ의 posterior distribution에 대한 quantiles의 기대 가치의 분산으로 정의

2.2.3. Decomposition of Uncertainties
- 반환값의 분포에 대한 전체 uncertainty는 두 uncertainties의 합으로 나타낼 수 있음
- Proposition 2.2.
- 식 4, 식 5의 σepistemic, σaleatoric을 통해 전체 uncertainty를 다음과 같이 구할 수 있음
- varθ,i(yi(θ,s,a))=σ2epistemic+σ2aleatoric
2.3. Approximate Uncertainties Using Two Networks
- 두 uncertainties를 위해 θ에 대한 분산과 기대값을 추정하는 것은 많은 수의 θ에 대한 샘플링을 수행해야 함 → 실용적이지 못함
- 대신 본 논문에서는 θ에 대한 posterior distribution으로부터 두 샘플 θA, θB를 통해 σ2epistemic, σ2aleatoric을 근사

- Proposition 2.3
- ˜σepistemic과 ˜σaleatoric은 σepistemic과 σaleatoric의 unbiased estimators

- Figure 1에서는 toy dataset에 대한 ˜σepistemic과 ˜σaleatoric을 살펴볼 수 있음
- 데이터가 있는 부분에서는 ˜σepistemic의 값이 작지만 데이터와 멀어질수록 그 값이 커짐
- ˜σaleatoric의 경우 데이터의 노이즈를 정확하게 나타냄
2.4. Uncertainty-Aware Deep Q Network

- 본 논문에서는 간단한 uncertainty-aware Deep Q Network (UA-DQN) 알고리즘을 제안 (QR-DQN을 기반으로 함) → 알고리즘은 Algorithm 1을 참고
Auxiliary networks for uncertainty estimation
- 가치 학습과 uncertainty 추정을 위해 본 논문에서는 두개의 auxiliary network θA, θB를 사용
- QR-DQN의 타겟 학습을 위해서도 사용
- 해당 네트워크들은 ˜σepistemic과 ˜σaleatoric을 구하기 위해 사용됨
Uncertainty-Aware Action Selection
- 추정된 uncertainty를 통해 risk awareness와 탐험 수행
- ˜σaleatoric 는 높은 분산을 가지는 행동을 penalize 하는데 사용
- ˜σepistemic는 Thompson sampling을 통해 탐험을 수행
3. Experiments
3.1. Safe Learning
- Uncertainty aware DQN을 AI Safely Gridworlds에 적용
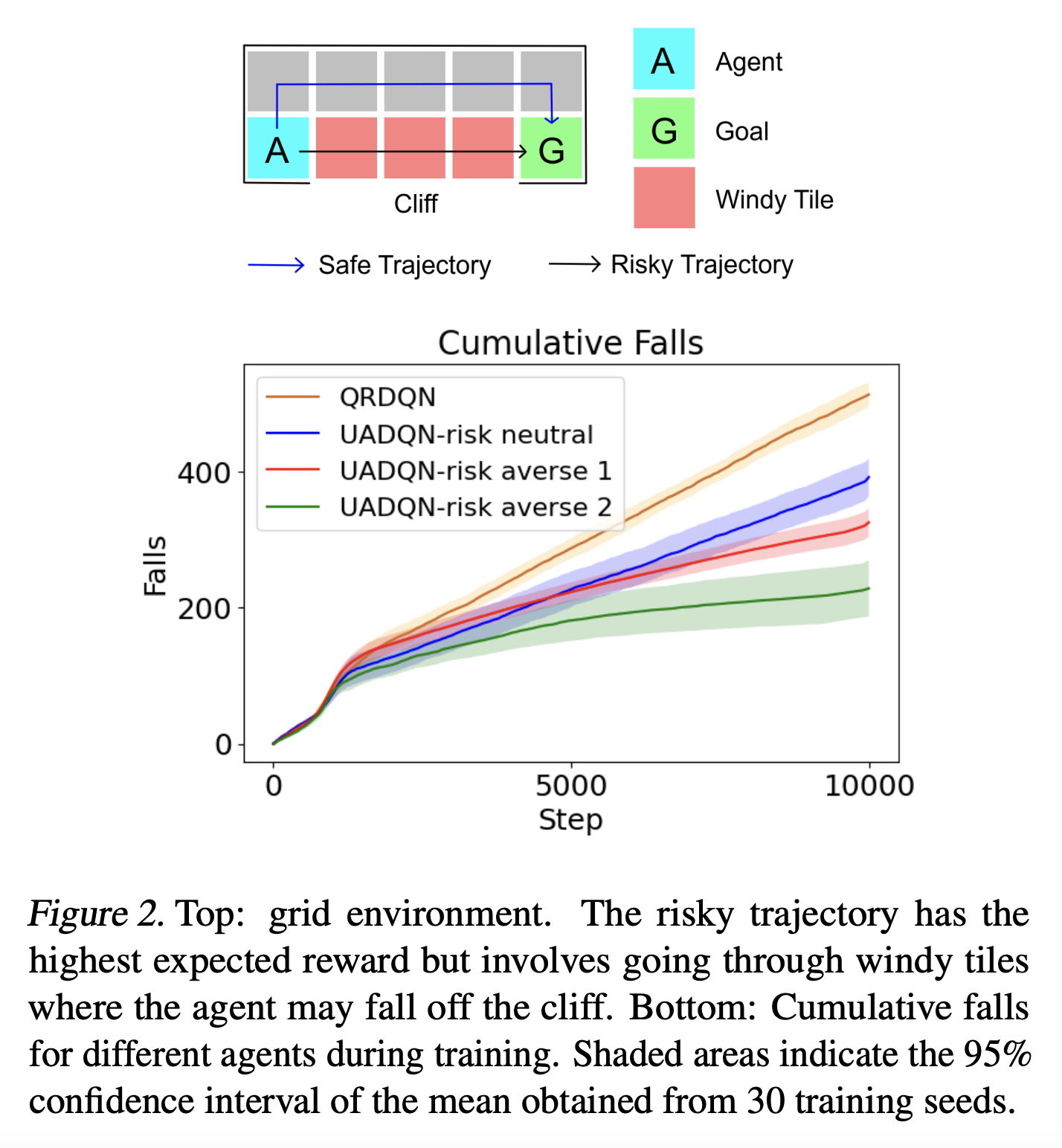
- 2x5 gridworld (Figure 2)
- 에이전트는 절벽에서 떨어지지 않고 골에 도착해야함
- 에이전트는 매 스텝 -1의 보상을 받고 골에 도달하면 +10의 보상을 받음
- 에이전트가 절벽에서 떨어지는 환경이 재시작
- 에이전트가 Windy tile에 있으면 5%의 확률로 에이전트를 절벽으로 떨어트림
- 위험한 경로로 가는 경우 반환값에 대한 기대 가치는 4.8, 안전한 경로의 반환값은 deterministic하게 4
- 본 논문에서 비교를 위해 사용하는 알고리즘들
- ϵ-greedy QR-DQN
- Risk-neutral version of UA-DQN (with λ=0)
- Two risk-averse variants of UA-DQN (with λ=0.5)
- 학습된 quantile들의 분산을 aleatoric uncertainty 추정에 사용
- ˜σaleatoric estimator 사용
- 실험 결과를 Figure 2에서 살펴볼 수 있음
- QR-DQN의 경우 risky trajectory, ϵ-greedy 때문에 가장 절벽에서 많이 떨어짐
- Risk-neutral UA-DQN의 경우 risky trajectory를 선택하게 되면서 절벽에서 떨어짐
- UA-DQN의 risk-averse variant 들은 안전한 경로를 사용하도록 학습
- Variant 1의 경우 aleatoric uncertainty를 너무 크게 추정 → biased estimator 이므로→ safe trajectory를 파악하는데 더 오래 걸리고 학습 동안 절벽에서 더 많이 떨어짐
- Variant 2의 경우 두 uncertainty에 대해서 unbiased estimator를 사용하므로 학습 동안 가장 적게 절벽에서 떨어짐
3.2. Evaluation on MinAtar
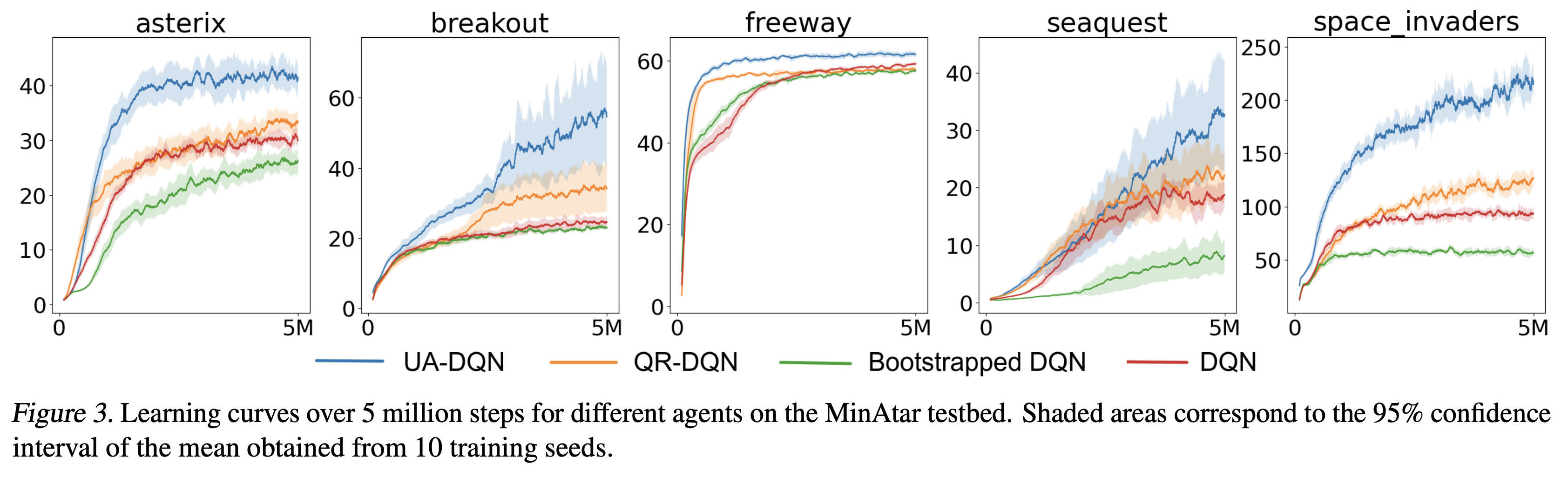
- MinAtar 환경에서 테스트 수행 → 5가지 Atari 게임의 단순화된 버전
- 유사한 게임 dynamics를 가지지만 더 낮은 차원의 관측을 가짐
- 성능 비교를 위해 사용한 알고리즘
- risk-neutral UA-DQN (λ=0), DQN, QR-DQN, Bootstrapped DQN
- 모든 알고리즘은 동일한 코드 베이스와 하이퍼파라미터를 가짐
- Adam optimizer 사용 → learning rate = 10−4
- 최종 ϵ=0.03 (DQN, QR-DQN, Bootstrapped DQN)
- β=0.2 (UA-DQN)
- Figure 3의 결과를 보면 QR-DQN이 다른 DQN variant에 비해 좋은 성능을 보임
- UA-DQN과 QR-DQN의 차이점을 행동을 선택하는 방법 밖에 없음 → 이를 통해 UA-DQN이 성공적으로 ˜σepistemic를 사용하여 적절한 탐험 및 greedy action을 선택한다는 것을 알 수 있음
4. Conclusion
- 두 uncertainties를 추정하는 것은 에이전트가 효율적인 탐험을 하는 것과 행동에 대한 risk를 고려하는데 사용할 수 있음
- 정책의 기대 반환에 대한 두 종류의 uncertainty는 deep RL에서도 추정될 수 있음
- 또한 본 논문에서는 오직 두개의 네트워크를 사용하여 이런 uncertainties에 대한 unbiased estimator를 제안 → 개선된 risk-sensitivity와 탐험을 위한 uncertainty-aware DQN 알고리즘 제안
- UA-DQN이 MinAtar 테스트 환경에서 다른 DQN 기반 알고리즘보다 좋은 성능을 보이는 것을 확인
'논문 리뷰 > Reinforcement Learning' 카테고리의 다른 글
| BYOL-Explore: Exploration by Bootstrapped Prediction (4) | 2024.11.03 |
|---|---|
| Planning with Diffusion for Flexible Behavior Synthesis (0) | 2024.11.03 |
| [Sampled MuZero] Learning and Planning in Complex Action Spaces (0) | 2024.10.15 |
| [MuZero] Mastering Atari, Go Chess and Shogi by Planning with a Learned Model (2) | 2024.09.22 |
| [M-RL] Munchausen Reinforcement Learning (1) | 2024.09.16 |



