
- Link: https://www.nature.com/articles/s41586-020-03051-4#MOESM1
- ArXiv link: https://arxiv.org/pdf/1911.08265.pdf
- Sudo Code
- pseudocode.py
0. Abstract
- Planning 능력을 가진 에이전트를 구축하는 것은 인공지능이 오랫동안 추구해 온 main challenge 중 하나
- Tree-based planning 기법의 경우 perfect simulation의 제공이 가능한 체스나 바둑 환경과 같은 도전적인 도메인에서 대단한 성공을 거둠
- 그러나 실제 문제들은 환경에 대한 dynamics가 복잡하고 알려져있지 않음
- 본 논문에서는 MuZero 알고리즘을 소개
- tree based search를 leared model과 결합
- 도전적이고 시각적으로 복잡한 도메인에서 dynamics에 대한 지식 없이 superhuman 성능 달성
- MuZero 알고리즘은 planning과 관련된 예측을 수행하는 iterable 모델을 학습
- Prediction 요소: action-selection policy, value function, reward
- 57개의 Atari 게임을 통해 성능 검증
- model-based planing 접근이 역사적으로 풀기 어려웠던 비디오 게임 환경
- MuZero 알고리즘의 경우 SOTA 성능을 보임
- 바둑, 체스, 장기 환경을 통한 성능 검증
- 높은 성능의 planning을 요구하는 환경
- MuZero 알고리즘은 게임 dynamics에 대한 지식 없이도 AlphaZero 알고리즘과 유사한 성능 달성
1. Introduction
- Planning 알고리즘
- lookahead search를 기반으로 하는 planning 알고리즘은 인공지능에서 굉장한 성공을 달성
- 체커, 체스, 바둑, 포커 등의 고전적인 게임에서 인간 세계 챔피언을 상대로 승리
- 실생활의 문제에도 적용 가능 → 물류, chemical synthesis
- 그러나 planning 알고리즘은 환경의 dynamics에 대한 지식에 의존 (시뮬레이터나 게임의 규칙) → 이런 이유로 일반적으로 실생활의 도메인 중 dynamics를 알수없는 robotics, inustrial control, intelligence assistance와 같은 환경에는 적용이 어려움
- Model-based RL
- 환경의 dynamics에 대한 모델을 먼저 학습하고 이렇게 학습된 모델을 이용하여 planning 수행
- 일반적으로 이런 모델들은 실제 환경의 상태나 모든 관측의 sequence를 reconstruction하는 것에 집중!
- 기존의 연구들은 Atari 2600과 같은 visually rich domain에서 좋은 성능을 보이지 못함
- 대신 model-free RL 기법들이 이런 환경에서 좋은 성능을 보임 → 환경과 상호작용 하면서 optimal policy와 value 추정
- 그러나 model-free 알고리즘은 체스나 바둑같이 정확하고 복잡한 lookahead가 요구되는 도메인에서는 좋은 성능을 보이지 못함
- MuZero
- Model-based RL 알고리즘
- Atari 2600에서 SOTA 성능 → 시각적으로 복잡한 도메인
- 게임 dynamics에 대한 지식 없이 체스, 장기, 바둑에서 superhuman 성능 → 정확한 planning이 필요한 도메인
- AlphaZero의 강력한 탐색과 policy iteration 알고리즘을 기반으로 하며 학습 과정에 learned model을 적용
- MuZero 알고리즘의 메인 아이디어 (Fig. 1에 요약)
- 모델이 관측 (바둑판이나 아타리 게임 이미지)을 입력으로 받고 이를 hidden state로 변환
- hidden state는 recurrent한 과정을 통해 iterative하게 업데이트 → 이전의 hidden state와 가상의 행동을 받음
- 모든 각 스텝에서 모델은 다음의 요소들을 도출
- policy: 플레이하기 위한 행동 예측
- value function: 누적 보상 예측
- immediate reward: 즉각적인 보상 예측
- 모델은 이런 요소들을 각각의 objective를 통해 학습
- improved policy and value function → MCTS의 예측
- 관측된 보상
- hidden state를 위한 요구사항
- 환경의 실제 state를 맞출 필요 없음
- state의 semantic에 대한 어떤 다른 constraint도 없음
- hidden state는 정확하게 policy, value function, reward를 예측할수만 있으면 되고 자유롭게 어떤 state도 나타낼 수 있음
Fig. 1 설명

- Fig 1. Planning, acting anc training with a learn model
- 어떻게 MuZero가 모델을 사용하여 plan하는지 보여줌
- 모델은 3개의 연결된 요소로 구성됨 → representation, dynamics, prediction
- 이전의 hidden state sk−1과 candidate action가 주어지면 dynamics function g는 immediate reward rk와 새로운 hidden state sk를 도출
- policy pk와 value function vk는 hidden state sk를 입력으로 한 prediction function f를 통해 예측
- 초기 hidden state s0는 과거의 관측들을 representation function h에 통과시켜서 취득
- 어떻게 에이전트가 환경에서 행동을 취하는지 보여줌
- 매 timestep마다 a에서 설명한 MCTS 연산 수행
- search policy π로부터 행동 at+1이 샘플링 → root node에서 각 행동에 대한 visit count에 비례하여 결정
- 환경에서 행동을 취해 새로운 관측 ot+1과 보상 ut+1 취득
- 매 에피소드의 마지막에 trajectory data가 replay buffer에 저장됨
- 어떻게 MuZero가 모델을 학습하는지 보여줌
- trajectory가 replay buffer에서 샘플링 됨
- 첫 스텝에서 representation function h는 선택된 trajectory에서 과거의 관측들 o1,...,ot를 입력으로 받음
- 모델은 K 스텝 동안 순차적으로 재귀적 unroll을 수행 (The model is subsequently unrolled recurrently for K steps)
- 각 k 스텝에서 dynamics function g는 이전 스텝으로부터의 hidden state sk−1과 실제 행동 at+k를 입력으로 함
- Representation, dynamics, prediction function들의 파라미터들은 세개의 값을 예측하도록 joint하게 end to end로 학습
- policy pk≈πt+k, value function vk≈zt+k, reward rk≈ut+k
- zt+k는 sampled return: final reward (보드 게임)이나 n-step return (아타리)
- 어떻게 MuZero가 모델을 사용하여 plan하는지 보여줌
2. MuZero Algorithm
- MuZero 알고리즘에 대해 더 자세히 살펴보자!
- 매 time step t에서 진행되는 각 예측은 모델 μθ (파라미터: θ)를 통해 k=0,...,K step에 대해 수행
- 과거의 관측들인 o1,...,ot에 conditioned되어 k>0에 대해 미래의 행동 at+1,...,at+k 예측
- 모델은 3가지 미래 요소들을 예측
- policy pkt≈π(at+k+1|o1,...,ot,at+1,...,at+k)
- value function vkt=E[ut+k+1+γut+k+2+...|o1,...,ot,at+1,...,at+k]
- immediate reward rkt≈ut+k
- u는 true, observed reward
- π는 실제 행동을 선택하기 위한 policy
- γ는 discount function
- MuZero는 3가지 모델을 사용 → representation function, dynamics function, prediction function
- Dynamics function (gθ)
- Recurrent process
- rk,sk=gθ(sk−1,ak)를 통해 매 가상의 스텝 k마다 immediate reward rk와 internal state sk 계산
- 기존의 model based RL과는 다르게 이 internal state sk는 환경의 상태에 대한 semantic을 가지지 않음 → 이는 단순하게 hidden state의 목적이 미래의 policy, value, reward 값을 잘 예측하는 것이기 때문
- 본 논문에서 dynamics function은 deterministic하게 구성 → stochastic transition으로 확장하는 것은 future work로
- Prediction function (fθ)
- internal state sk로부터 policy와 value function 계산
- pk,vk=fθ(sk)
- Representation function (hθ)
- 과거의 관측을을 encoding하여 ‘root’ state s0를 초기화
- s0=hθ(o1,...,ot)
- Dynamics function (gθ)
- 이런 모델이 주어지면 주어진 과거의 관측들 o1,...,ot를 통해 가상의 미래 trajectory a1,...,ak를 탐색하는 것이 가능함
- 본 논문에서는 AlphaZero의 search와 유사하게 MCTS 알고리즘을 적용하여 탐색을 수행
- MCTS 알고리즘은 search policy πt=P[at+1|o1,...,ot]와 search value function vt≈E[ut+1+γut+2+...|o1,...,ot]로 볼 수 있음 → 두 function 모두 주어진 과거의 관측들 o1,...,ot를 통해 행동을 선택하고 누적 보상을 예측
- 각 internal node에서 policy, value function, reward 예측이 현재 모델 파라미터 θ를 통해 얻어지고 이 값들을 결합하여 lookahead search 수행 → search tree의 root에서 개선된 policy πt와 개선된 value function vt를 얻을 수 있음
- 다음 행동 at+1≈πt 는 search policy에 의해 선택됨
- 모델의 모든 파라미터들은 모든 가상의 스텝 k에 대해 policy, value function, reward 예측이 실제 k 스텝 후에 관측된 3개의 타겟을 정확히 맞추도록 한꺼번에 학습됨
- 첫번째 objective는 policy pkt에 의해 예측된 행동과 search policy πt+k를 통해 예측된 행동 사이의 에러를 최소화하는 것
- 또한 AlphaZero와는 다르게 value target은 게임을 플레이하거나 search policy를 사용한 MDP를 통해 생성 → 그러나 AlphaZero는 n-step return zt를 사용 (zt=ut+1+γut+2+...+γn−1ut+n+γnvt+n)
- 보드게임에서 최종결과는 {lose, draw, win} → episode의 마지막 스텝에서 발생하는 보상 ut∈{−1,0,1}
- 두번째 objective는 value function vkt와 value target zt+k 사이의 오차를 최소화하는 것
- 세번째 objective는 예측된 immediate reward rkt와 관측된 immediate reward ut+k 사이의 오차를 최소화
- 마지막으로 L2 regularization을 더해주고 상수 c를 통해 scale
- 첫번째 objective는 policy pkt에 의해 예측된 행동과 search policy πt+k를 통해 예측된 행동 사이의 에러를 최소화하는 것
- 최종 loss
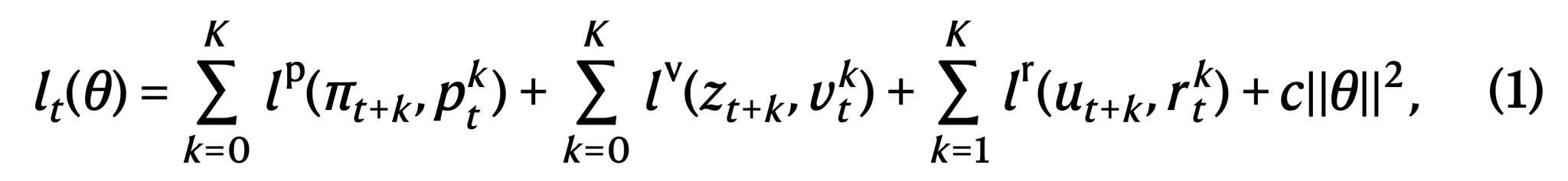
- lp,lv,lr은 각각 policy, value, reward에 대한 loss function
- Supplementary Fig. 2에 MuZero의 plan, act, learn과 관련된 수식들을 살펴볼 수 있음 (Supplymentary Fig와 table들은 본 문서 가장 하단에 추가)
- Chess, Go, Shogi
- AlphaZero와 같이 reward, value를 위해 squared error loss 사용
- policy를 위해서는 cross-entropy loss 사용
- Atari
- reward와 value를 위해 cross entropy loss를 사용하는 것이 squared error loss를 사용하는 것 보다 안정적
- policy를 위해 cross entropy loss 사용
3. Results
- MuZero 알고리즘은 다음의 환경들에서 성능 검증
- 바둑, 체스, 장기 → 어려운 planning 문제들
- 57개의 Atari 환경 → 시각적으로 복잡한 도메인
- 각 경우마다 MuZero 알고리즘은 K=5의 가상 스텝에 대해 학습 진행
- 백만 미니배치 학습 수행 → batch size: 2048 (보드 게임), 1024 (아타리)
- Muzero의 simulation 수행 → 800 (보드 게임), 50 (아타리)
- 네트워크 구조
- Representation function: AlphaZero와 동일한 convolution과 residual 구조 (residual block은 20 대신 16개 사용)
- Dynamic function: representation function과 동일한 구조 사용
- Prediction function: AlphaZero와 동일한 구조 사용
- 모든 네트워크는 256 hidden plane 사용 (이후에 Method 부분에서 더 자세히 설명)
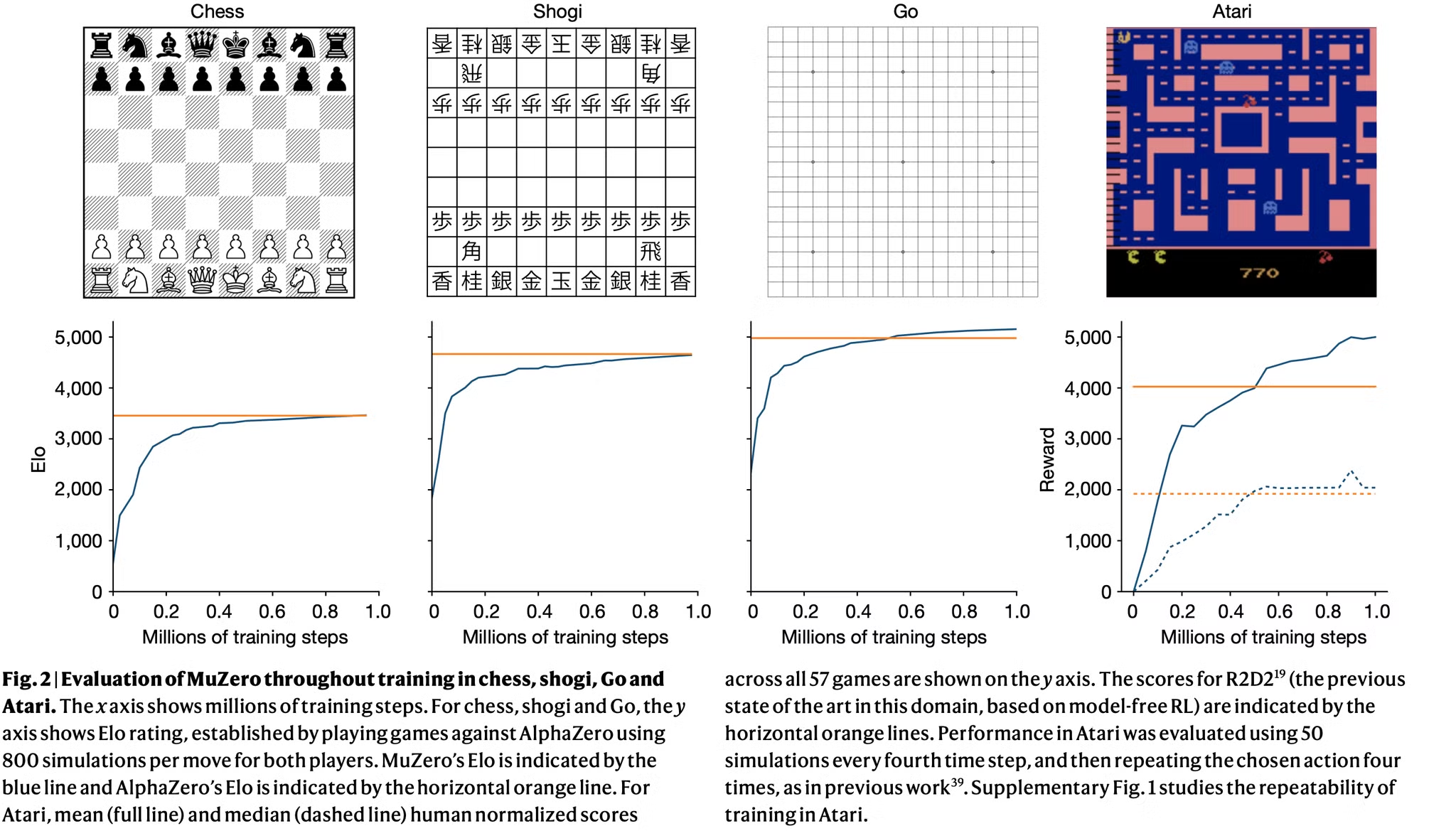
- Fig. 2는 각 게임에서 학습동안 성능의 변화를 보여줌
- 바둑에서는 MuZero가 AlphaZero 보다 조금 더 높은 점수를 보여줌
- AlphaZero보다 더 적은 연산 사용 (16 residual blocks)
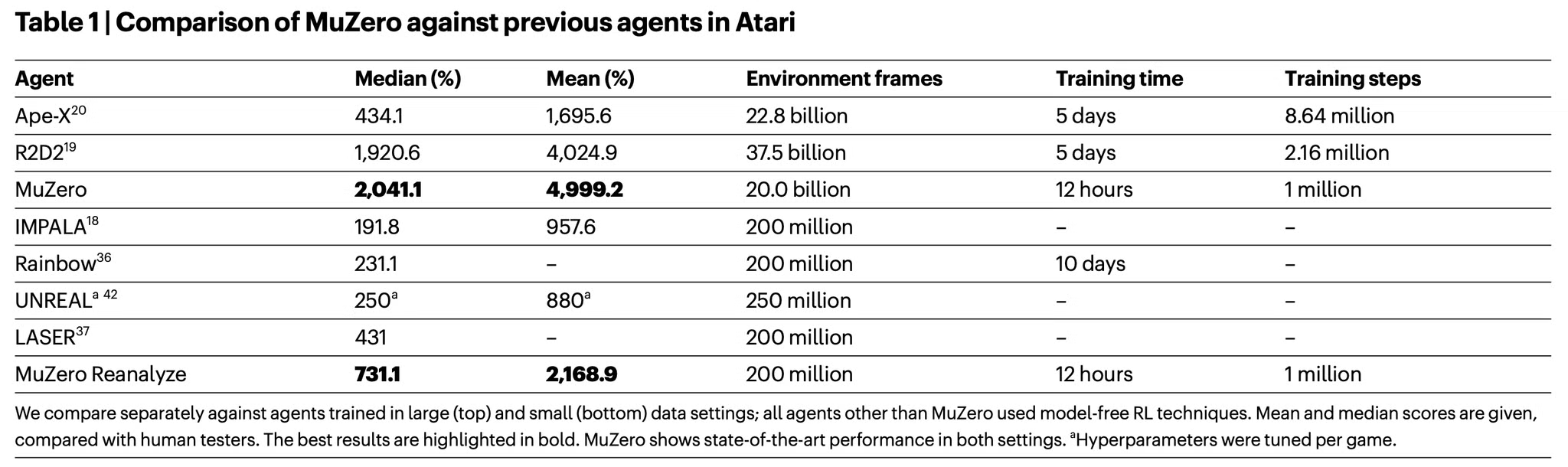
- Atari에서는 MuZero가 57개의 게임에서 mean, median normalized score 모두 SOTA 성능을 보임
- 57개 중 47개의 게임에서 기존의 SOTA인 R2D2에 비해 더 좋은 성능을 보임
- 또한 기존의 model based 기반 알고리즘 중 가장 좋은 성능을 보인 SimPLe보다 좋은 성능 보임 (Table1, Supplementary Table 1 참고)
- 바둑에서는 MuZero가 AlphaZero 보다 조금 더 높은 점수를 보여줌
- 또한 sample efficiency를 향상시키도록 최적화한 두번째 버전의 MuZero 평가
- old trajectory에 대해 최신의 네트워크를 사용한 MCTS를 다시 적용하여 신선한 target을 도출
- Method의 ‘MuZero Realanyze’ 참고
- 57개의 아타리 게임에 대해 200M frame 동안 학습 진행
- MuZero Reanalyze는 731%의 median normalized socre를 얻었고 이외의 알고리즘들은 192% (IMPALA), 231% (Rainbow), 431% (LASER)를 달성
- MuZero에서 모델의 역할을 이해하기 위해 바둑, 아타리의 Ms. Pac-Man 게임에서 몇가지 실험을 수행
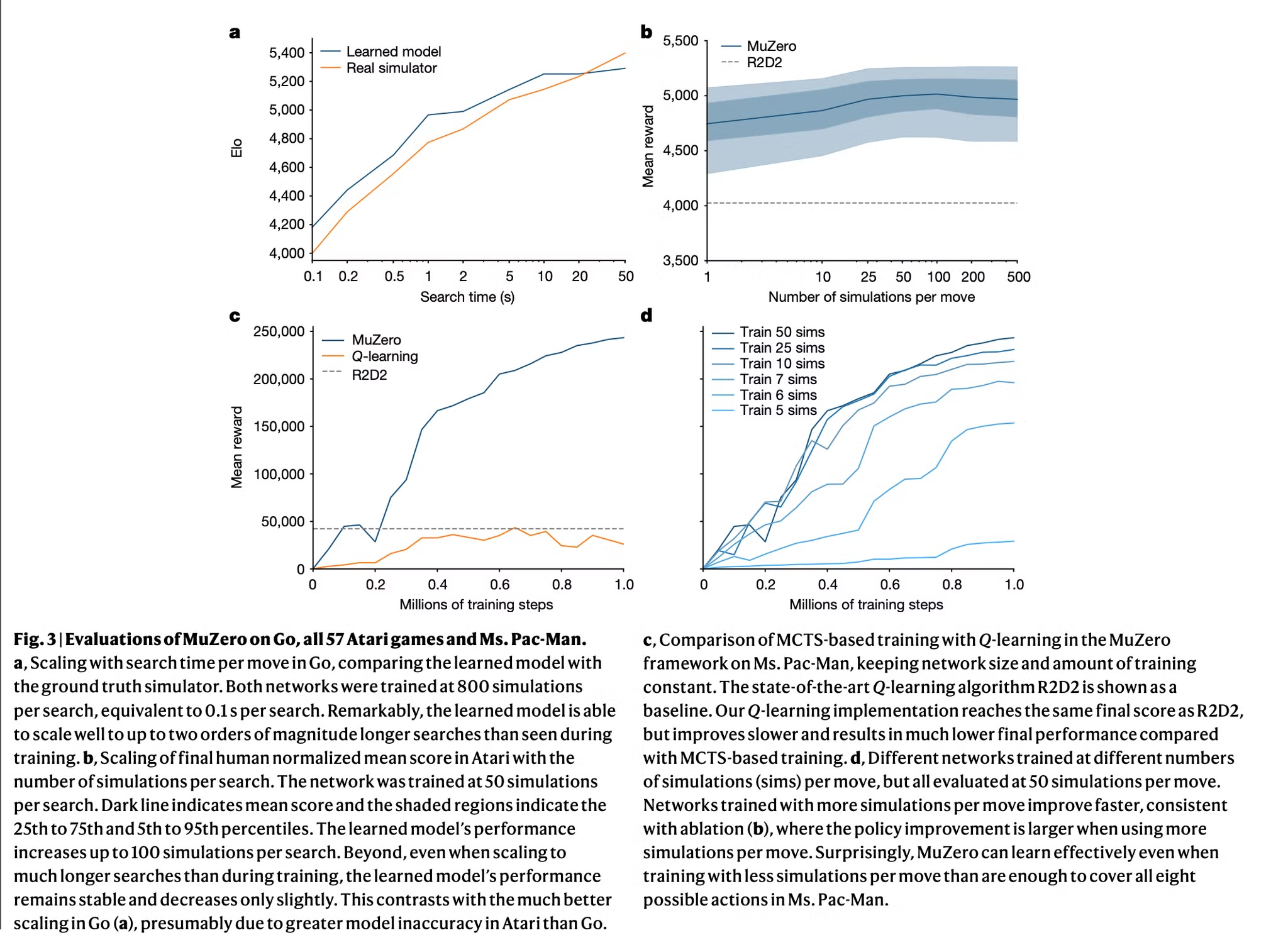
- 첫번째로 바둑에서 planning의 scalability 테스트 (Fig. 3a)
- Learned model을 사용하는 MuZero와 perfect model을 사용하는 AlphaZero 알고리즘의 탐색 성능 비교
- 구체적으로 완전히 학습된 AlphaZero나 MuZero의 MCTS 비교 검증
- MuZero와 학습시에서는 0.1로 정도의 thinking time만을 통해서 학습했음에도 불구하고 깊은 search를 수행하는 경우 (10초 이상)에도 perfect 모델과 유사한 성능을 보임
- Supplymentary Fig. 3a 참고
- 두번째로 모든 아타리 게임에서 planning의 scalability 테스트 (Fig. 3b)
- 완전히 학습된 MuZero가 MCTS 수행시 simulation의 수를 다르게 하여 성능 비교
- Planning에 따른 성능의 향상이 바둑에 비해서는 크게 뚜렷하지는 않음 (model의 부정확도가 더 크기 때문)
- 탐색 시간에 따라 성능이 조금씩 향상되지만 100 sim 이후로는 정체기가 옴
- Policy network에 의해서 바로 행동을 결정하는 single simulation의 경우에도 MuZero는 좋은 성능을 보임 → 학습이 끝나면 raw policy도 탐색의 이점을 이미 내재화하도록 학습
- Supplymentary Fig. 3b 참고
- 세번째로 model-free 학습 알고리즘 대비 model-based 학습 알고리즘의 성능 테스트 (Fig. 3c)
- MuZero의 objective (eq. 1)을 model-free Q-learning의 objective (R2D2)로 변경하고 성능 비교
- dual policy, value head도 single head representating action-value function으로 변환
- 학습과 평가에도 탐색을 수행하지 않음
- Ms. Pac-Man에서 평가했을 때 model-free 알고리즘은 R2D2와 유사한 성능 달성 → 하지만 MuZero보다 훨씬 느리게 학습했으며 최종 성능도 더 낮음
- 위 결과를 통해 MuZero의 탐색 기반 policy improvement step이 큰 bias, variance를 가지는 Q-learning 기반의 target에 비해 강력한 학습 signal을 제공하는 것을 알 수 있음
- 학습 동안 사용하는 탐색의 양에 따라 어떻게 MuZero의 학습이 scale되는지 측정 (Fig. 3d)
- 학습 동안 MCTS에서 다른 수의 simulation을 사용하는 것이 다른 성능 향상을 보여줌
- Ms. Pac-Man에서는 놀랍게도 행동의 수보다 적은 6 simulation 만으로도 빠르게 효율적인 policy를 학습
- 더 많은 simulation을 수행하면 성능이 더 빠르게 향상됨
- 각각의 개별적인 iteration 동안 policy improvement에 대한 분석은 Supplementary Fig. 3c, d 참고
- 첫번째로 바둑에서 planning의 scalability 테스트 (Fig. 3a)
4. Conclusions
- 인공지능에서 많은 breakthrough들은 높은 성능의 planning이나 model-free RL 기법을 기반으로 해왔음
- 본 논문에서는 두가지 접근의 장점을 결합한 기법을 소개
- 본 논문의 알고리즘, MuZero는 논리적으로 복잡한 보드 게임 (바둑, 체스, 장기)에서 사람의 성능을 뛰어넘는 성능을 보였을 뿐 아니라 시각적으로 복잡하여 최신 model free 알고리즘이 좋은 성능을 보인 Atari 게임에서도 SOTA 성능 보임
- 또한 본 기법은 환경 dynamics에 대한 지식을 요구하지 않음
- 위와 같은 특성에 따라 완벽한 시뮬레이터가 없는 실세계 기반의 도메인에서도 강력한 모델 기반 planning과 학습 성능을 보일 수 있음
Methods
A. Comparison to AlphaZero
- MuZero는 AlphaGo Zero나 AlphaZero에 비해 더 일반적인 세팅
- AlphaGo Zero와 AlphaZero의 plnanning 과정에서 시뮬레이터를 사용하여 next state, reward를 샘플링 → 환경의 dynamics와 게임의 룰에 따름
- 시뮬레이터는 search tree 내부에서 게임의 상태를 업데이트 (Fig. 1a)
- 시뮬레이터는 3가지 중요한 정보를 제공
- search tree 내부의 state transition
- search tree의 각 node에서의 available action
- search tree 내부에서 에피소드 종료
- MuZero에서는 위의 모든 정보들이 neural network에 의해 학습된 단일 implicit model을 사용하는 것으로 대체됨
- state transitions
- AlphaZero는 환경의 dynamics에 대한 perfect simulator를 사용
- MuZero는 search 수행에서 학습된 dynamics model을 사용
- 이 모델을 사용할 떄 tree의 각 node는 이와 연관된 hidden state로 나타냄
- hidden state sk−1과 action ak를 모델에 적용하여 search 알고리즘은 새로운 node로 transition 할 수 있음 → sk=g(sk−1,ak)
- Action Available
- Search 동안 각 내부 node에서 available action을 아는 것은 도움이 될 수 있음 → 이를 위해서는 시간의 변화에 따라 available action이 어떻게 되는지 알아야 함
- AlphaZero는 simulator를 통해 legal action을 취득하여 interior node에서 policy network를 masking
- MuZero는 search tree 내에서 어떤 masking도 수행하지 않지만 root 노드에서는 available action의 set이 직접적으로 관측가능하므로 legal action에 대한 masking 진행
- Policy network는 불가능한 행동은 빠르게 제외하도록 학습 → 단순히 선택이 불가능하기 때문
- Terminal states
- AlphaZero는 terminal state의 tree node가 되면 search를 중단, terminal value는 시뮬레이터를 통해 제공
- MuZero는 terminal state에 대한 특별한 조치를 취하지 않음 → 항상 network를 통해 예측된 value만을 사용
- 이 경우 네트워크는 항상 동일한 value를 예측할 것으로 기대됨, 이는 학습 동안 absorbing states로 terminal state를 모델링 하도록 달성됨 (?) (원문: In this case, the network is expected to always predict the same value, which may be achieved by modelling terminal states as absorbing states during training)
- state transitions
- 추가적으로 MuZero는 일반적인 강화학습 환경에서 작동하도록 디자인 됨
- single agent domain with discounted intermediate rewards of arbitrary magnitude
- 대조적으로 AlphaGo Zero와 AlphaZero는 두명의 플레이어가 대결하는 게임을 위해 디자인 되었고 감가되지 않은 terminal reward ±1 사용
- MuZero의 경우 많은 generalization이 가능함
- stochastic, continuous, non-stationary, temporally extended environments, imperfect information, general sum game
- 위의 요소들은 future work로 남겨둠
B. Search
- MuZero의 search 알고리즘에 대해 설명
- 본 논문의 접근은 upper confidence bound를 적용한 MCTS를 기반으로 함
- single agent domain과 zero sum game에서 minimax value function에서 점근적으로 최적의 policy로 수렴할 수 있도록 planning
- Search tree의 모든 노드는 internal state s 사용 → 각 s로부터 action a가 각 edge (s,a)가 되며 다음의 정보들 (statistics)을 저장 → {N(s,a),P(s,a),Q(s,a),R(s,a),S(s,a)}
- N: visit count, P: policy, Q: mean value, R: reward, S: state transition
- AlphaZero와 유사하게 search는 다음의 세가지 과정으로 나눠지고 시뮬레이션 동안 반복됨
- Selection, Expansion, Backup
Selection
- 매 simulation은 internal root state s0부터 시작하고 leaf node sl이 되면 simulation 종료
- 시뮬레이션의 각 가상의 time step k=1,...,l 동안 internal state sk−1에 저장된 데이터를 기반으로 probabilistic upper confidence tree (PUCT) bound가 최대가 되도록 행동 ak가 선택
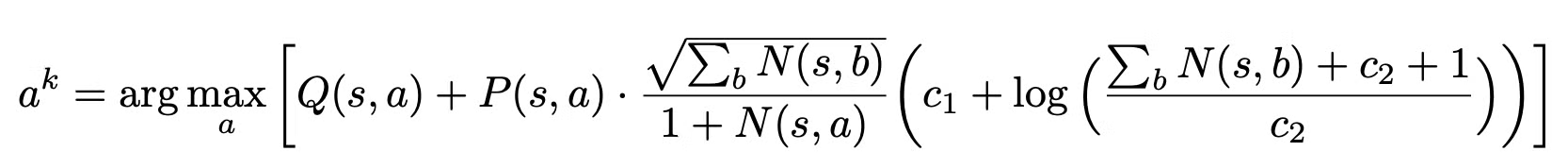
- a,b는 가능한 행동들
- c1,c2는 value Q(s,a)에 대한 policy P(s,a)의 영향을 조절 → 노드가 더 자주 방문되도록
- 본 논문의 실험에서는 c1=1.25,c2=19625로 사용
- k<l 일 때 다음 상태와 보상은 state transition과 reward table에 따라 탐색
- sk=S(sk−1,ak), rk=R(sk−1,ak)
Expansion
- simulation의 마지막 time step l
- dynamic function에 의해 reward와 state 계산 → rl,sl=gθ(sl−1,al)
- policy와 value function을 prediction function을 통해 계산 → pl,vl=fθ(sl)
- Search tree에 state sl에 해당하는 새로운 노드 추가
- 각 edge (sl,a)로부터 새로운 expanded node들이 다음과 같이 초기화
- {N(sl,a)=0,Q(sl,a)=0,P(sl,a)=pl}
Backup
- Simulation이 종료되면 trajectory를 따라 statistics 업데이트
- k=l,...,0에 대해 l−k step에 대한 cumulative discounted reward를 추정 → value function vl로부터 bootstrapping
- Gk=∑l−1−kτ=0γτrk+1+τ+γl−kvl
- k=l,...,1에 대해 다음과 같이 각 edge (sk−1,ak)의 statistics 업데이트
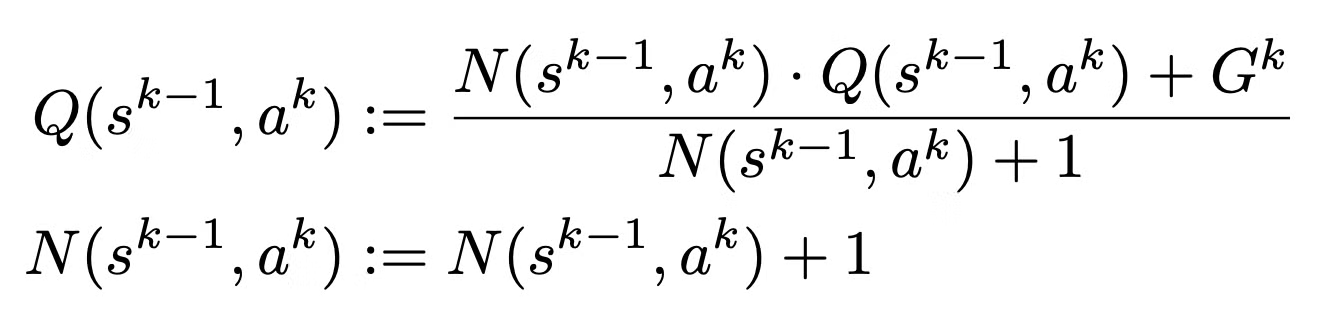
- two-player zero sum game의 경우
- value function이 [0,1]의 범위로 bounded
- 이 선택은 PUCT rule의 variant를 사용하여 추정 가치를 확률과 결합하도록 함
- 그러나 많은 환경에서 가치는 unbounded 되어있으므로 PUCT rule을 수정할 필요 있음
- 간단한 방법은 환경에서 관측되는 최대의 점수를 사용하여 value를 rescale하거나 PUCT 상수를 적절히 결정하는 것
- 그러나 두 방법 모두 게임 specific하고 MuZero 알고리즘에 prior knowledge를 추가하는 것
- 이를 피하기 위해 MuZero는 normalized Q-value 추정을 사용 → ˉQ∈[0,1]은 해당 시점까지 search tree에서 관측된 최소-최대의 가치를 사용
- Selection stage 동안 node에 도달하면 알고리즘은 normalized ˉQ values를 계산하고 edge의 Q-value를 대체
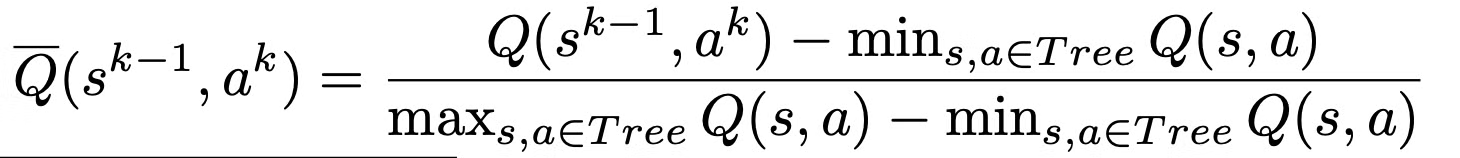
C. HyperParameters
- 기존의 연구와 동일한 구조와 하이퍼 파라미터 사용
- 보드게임의 경우 AlphaZero와 동일한 PUCT constant 사용, Dirichlet exploration noise 사용, 각 search 당 800 simulation 수행
- Atari에서는 더 적은 branching factor와 더 단순한 policy를 가지므로 search 당 50 simulation만 사용하여 실험의 속도 향상
- R2D2와 동일한 discount (0.997)과 value transformation 사용
- 본 논문에 나오지 않은 파라미터들은 pseudocode 참고
D. Data Generation
- 학습 데이터를 만들어 내기 위해 네트워크의 최신 체크포인트를 사용하여 MCTS를 통해 게임 플레이 (1,000 training step마다 업데이트)
- 바둑, 체스 장기 같은 보드 게임에서는 한번 행동 선택에 800 simulation 수행하고 Atari에서는 50 simulation 만으로 충분
- 저장되는 데이터의 양
- 보드 게임의 경우 한 게임이 끝나면 게임의 정보를 training job으로 보냄
- Atari game의 경우 길이가 길기 때문에 (up to 30 min or 108,000 frames) 중간 sequence들이 매 200 move마다 전송
- 보드 게임에서는 training job이 최근 100만 게임에 대한 정보를 replay buffer에 저장
- Atari의 경우 visual observation이 크기 때문에 200의 길이를 가지는 최근 125,000 sequence 저장
- 보드 게임에서 경험을 생성하는 동안 AlphaZero와 동일한 exploration 사용
- Atari에서는 action이 첫 k move 대신 visit count distribution을 통해 sample 됨
- Visit count distribution은 temperature parameter T를 통해 parameterized
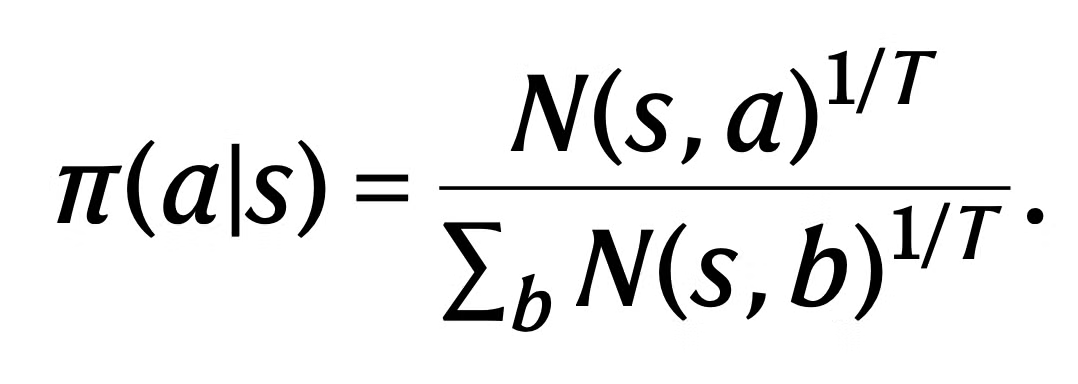
- T는 network에 대한 학습 스텝의 수에 따라 decay 됨
- 구체적으로 첫 500,000 training step 동안은 1.0을 사용하고 다음 250,000 스텝은 0.5, 나머지 250,000 스텝 동안은 0.25 사용
- 이를 통해 학습이 진행되는 동안 점점 greedy하게 행동을 선택할 수 있음
E. Observation and Action Encoding
Representation function
- 보드 게임의 경우 representation function의 입력으로 board 상태의 history 사용
- 바둑과 장기의 경우 AlphaZero와 마지막 8개의 board state 사용, 체스의 경우 마지막 100 bard state 사용 (무승부에 대한 정확한 예측을 위해)
- Atari의 경우 96x96 사이즈의 마지막 32개의 RGB 프레임을 마지막 32 action과 함께 사용
- 보드 게임과 다르게 action에 대한 history를 사용 → Atari에서 행동이 관측에 시각적인 효과를 주지 못할 수 있기 때문 (?) (an action in Atari does not necessarily have a visible effect on the observation)
- RGB frame들은 색당 하나의 plane으로 encoding → red, blue, green 각각에 대해 [0,1]의 범위로 rescale됨
- RBG input에 대해 다른 normalization이나 whitening 등은 수행하지 않음
- Historical action의 경우 simple bias plane으로 encoding → a/18로 scale 수행 (Atari에 총 18개의 행동이 있으므로)
Dynamics function
- Dynamics function의 입력은 representation function이나 이전의 dynamics function이 만들어낸 hidden state에 transition을 위한 action의 representation을 concatenate한 것
- 행동은 hidden state와 동일한 resolution으로 encoding
- Atari의 경우 6x6으로 보드게임의 경우 보드 사이즈와 동일 (바둑: 19x19, 체스: 8x8, 장기: 9x9)
- 바둑의 경우
- normal action은 played stone의 위치만 1이고 나머지는 0인 plane으로 인코딩
- pass는 all-zero plane으로 인코딩
- 체스의 경우
- 8개의 plane이 행동을 인코딩하는데 사용됨
- 첫번째 one-hot plane은 기물이 움직이기 시작한 위치를 인코딩
- 다음 두 plane은 기물이 움직인 위치를 인코딩 → 첫번째 one-hot plane은 target 위치를 인코딩, 두번째 binary plane은 타겟 위치가 유효한지 아닌지 인코딩
- 동일한 action space를 policy prediction과 dynamic function의 입력으로 사용
- 남은 다섯개의 binary plane은 promotion의 type을 나타냄 → (queen, knight, bishop, rook, none)
- 장기의 경우
- 총 11개의 plane 사용
- 첫 8 plane은 기물이 이동을 시작한 위치 혹은 drop of the seven types of prisoner (?) 을 나타냄
- 다음 2개의 plane은 target을 encoding
- 남은 binary plane은 이동이 promotion이었는지 아닌지 나타냄
- Atari의 경우
- 행동은 one-hot vector로 인코딩 → plane으로 적절하게 tiled
Network Architecture
- Prediction function pk,vk=fθ(sk)는 AlphaZero와 동일한 구조 사용
- Scaling & Transformation
- Atari에서 value와 reward prediction에서 target은 invertible transform을 수행
- h(x)=sign(x)(√|x|+1−1)+ϵx (ϵ=0.001)
- 그리고 transformation ϕ를 scalar reward와 value target에 적용하여 equivalent categorical representation을 얻음
- 601의 크기를 가지는 discrete support set을 사용 → -300 ~ 300의 정수
- 이 transformation에서 각 scalar는 두개의 인접한 support의 linear combination으로 표현
- x=xlow×plow+xhigh×phigh
- 예시: target이 3.7인 경우 → 0.33 + 0.74로 계산 (C51과 같음)
- 네트워크의 value와 reward output은 601의 크기를 가지는 softmax output으로 모델링
- During the inference, the actual value and rewards are obtained by first computing their expected value under their respective softmax distribution and subsequently by inverting the scaling transformation
- 이런 value와 reward에 대한 scaling과 transformation은 network 단에서 발생하며 알고리즘의 나머지에서는 보이지 않음
- Representation과 dynamics function 모두 AlphaZero와 동일한 구조 사용 → 20 residual block 대신 16 residual block 사용하고 각 convolution에 대해 3x3 kernel, 256 hidden plane 사용
- Atari에 대해서 observation이 large spatial resolution을 가지므로 representation function은 sequence of convolution을 stride 2로 시작하여 spatial resolution을 감소
- Input에서 observation의 resolution=96x96, 128planes (32 history frames of 3 colour channel, plane으로 broadcast한 32 actions를 concatenate)
- 이를 downsample → 1 convolution with stride 2 and 128 output planes → output resolution = 48x48
- 이후 네트워크 연산 과정 (모든 kernel size = 3x3)
- 2 residual blobks with 128 planes
- 1 convolution with stride 2 and 256 planes → output resolution=24x24
- 3 residual blocks with 256 planes
- average pooling with stride = 2 → output resolution = 12x12
- 3 residual blobks with 256 planes
- average pooling with stride = 2 → output resolution = 6x6
- Dynamics function에 대해서 (항상 downsampled resolution 6x6으로 연산) 행동은 처음에는 이미지의 형태로 encoding되고 이를 plane dimension으로 이전 스텝의 hidden state에 stack
Training
- 학습 동안에 MuZero 네트워크는 K hypothetical step 동안 unroll → MCTS actors에 의해 생성된 trajectories로부터 샘플링 된 sequces에 align
- Sequence들은 replay buffer 내부의 게임으로부터 state를 sampling 하도록 선택 → 그리고 해당 state로 부터 K step unroll 수행
- Atari에서 sample 들은 prioritized replay를 통해 추출
- priority P(i)=pαi∑kpαk where pi=|vi−zi|
- v는 search value, z는 observed n-step return
- Prioritized sampling에 의한 sampling bias 해결을 위해 importance sampling ratio를 사용하여 loss를 scale → wi=(1N×1P(i))β
- 본 논문에서 α=β=1로 설정
- 보드게임에서는 모든 상태가 uniform하게 샘플링
- Sequence의 각 관측 ot도 대응하는 search policy πt, search value function vt, environment reward ut를 가짐
- 각 unroll step k에서 네트워크는 해당 스텝에 대한 policy, value, reward target의 loss를 가짐 → 이를 모두 더하여 MuZero 네트워크의 전체 loss 계산
- 보드게임에서는 intermediate reward 없기 때문에 reward prediction loss는 제거
- 보드게임의 경우 최종 결과를 예측하는 것과 동일하게 게임의 끝으로 직접적으로 bootstrap
- Atari에서는 n=10 step의 미래에 대해 bootstrap
- 다른 unroll step들에 대해 거의 동일한 크기의 gradient를 유지하기 위해 gradient를 두개의 분리된 위치에서 scale
- 각 head의 loss를 1/K로 scale (K= unroll step의 수) → 이는 우리가 수행할 unroll의 수와 관계없이 전체 gradient가 유사한 크기를 가지도록 보장
- Dynamics function의 시작부분에서 gradient를 1/2로 scale → dynamics function에 적용되는 전체 gradient를 constant로 보장
- 본 논문에서는 K=5 step로 unroll
- 학습 과정을 개선하고 activation을 bound하기 위해 hidden state를 action input ([0,1])과 동일한 범위로 scale → sscaled=s−min
- 연산 관련 내용
- 모든 실험은 3세대의 Google Cloud tensor processing units (TPU) 사용
- 각 보드게임에서는 16 TPU를 학습에 사용하고 1000 TPU를 self-play에 사용
- 각 아타리 게임에서는 학습에 8 TPU (20 billion frame setting), 32 TPU를 self play에 사용
- 200 million frame setting에서는 오직 4개의 TPU를 학습에, 2개의 TPU를 self play에 사용
- 이는 1 GPU로 2주간 학습하는 것과 비슷한 시간
- 아타리에서 더 적은 수의 simulation (50 vs 800)을 수행하므로 더 적은 비율의 TPU를 사용
- 네트워크는 각 환경에 대해 독립적으로 학습 (다른 아타리나 보드 게임에 대해서 하나의 모델)
- 그러나 이론적으로는 학습 동안 다른 환경 사이에 동일한 모델을 공유할 수 있음 (zero-shot generalization) → future work
MuZero Reanalyze
- MuZero의 sample efficiency 향상을 위해 알고리즘의 두번째 variant인 MuZero Reanalyze 사용
- MuZero Reanalyze는 과거의 time step에 재방문 → 최신 모델 파라미터를 이용하여 search를 다시 수행
- 이를 통해 원래의 search보다 더 좋은 quality의 policy를 사용
- This fresh policy is used as the policy target for 80% of updates during MuZero training
- 또한 최신 파라미터 \theta^-를 기반으로 한 target network v^- = f_{\theta^-}(s^0)가 사용되어 value function에 대해 더 신선하고 안정된 n-step bootstrapped target를 계산 → z_t = u_{t+1}+\gamma u_{t+2}+...+\gamma^{n-1}u_{t+n}+\gamma^n v_{t+n}^-
- Sample reuse를 늘리고 value function의 overfitting을 방지하기 위해 추가적으로 몇몇의 다른 하이퍼파라미터들이 조정됨
- 상태 당 0.1 대신 2.0 samples가 drawn
- Policy와 reward target을 위해 사용하던 1.0의 weight와 비교하여 value target이 0.25로 weighted down
- n-step return이 10 step에서 5 step으로 감소
Evaluation
- 보드게임에서는 각 플레이어의 Elo rating으로 상대적인 강함을 평가
- player a가 player b를 이길 확률을 logistic function p로 예측
- p=(1+10^{c_{elo}[e(b)-e(a)]})^-1
- rating e(\cdot)은 BayesElo program을 통해 Bayesian logistic regression으로 예측 (standard constant c_{elo}=1/400 사용)
- Elo rating은 MuZero의 학습 동안 iteration 사이에 800 simulation per-move 토너먼트의 결과로 계산
- 또한 baseline player와도 도출: Stockfish, Elmo, AlphaZero
- player a가 player b를 이길 확률을 logistic function p로 예측
- 아타리에서는 게임마다 1000 에피소드에 대한 평균 보상 계산
- 에피소드 당 30분 혹은 108,000 프레임으로 제한
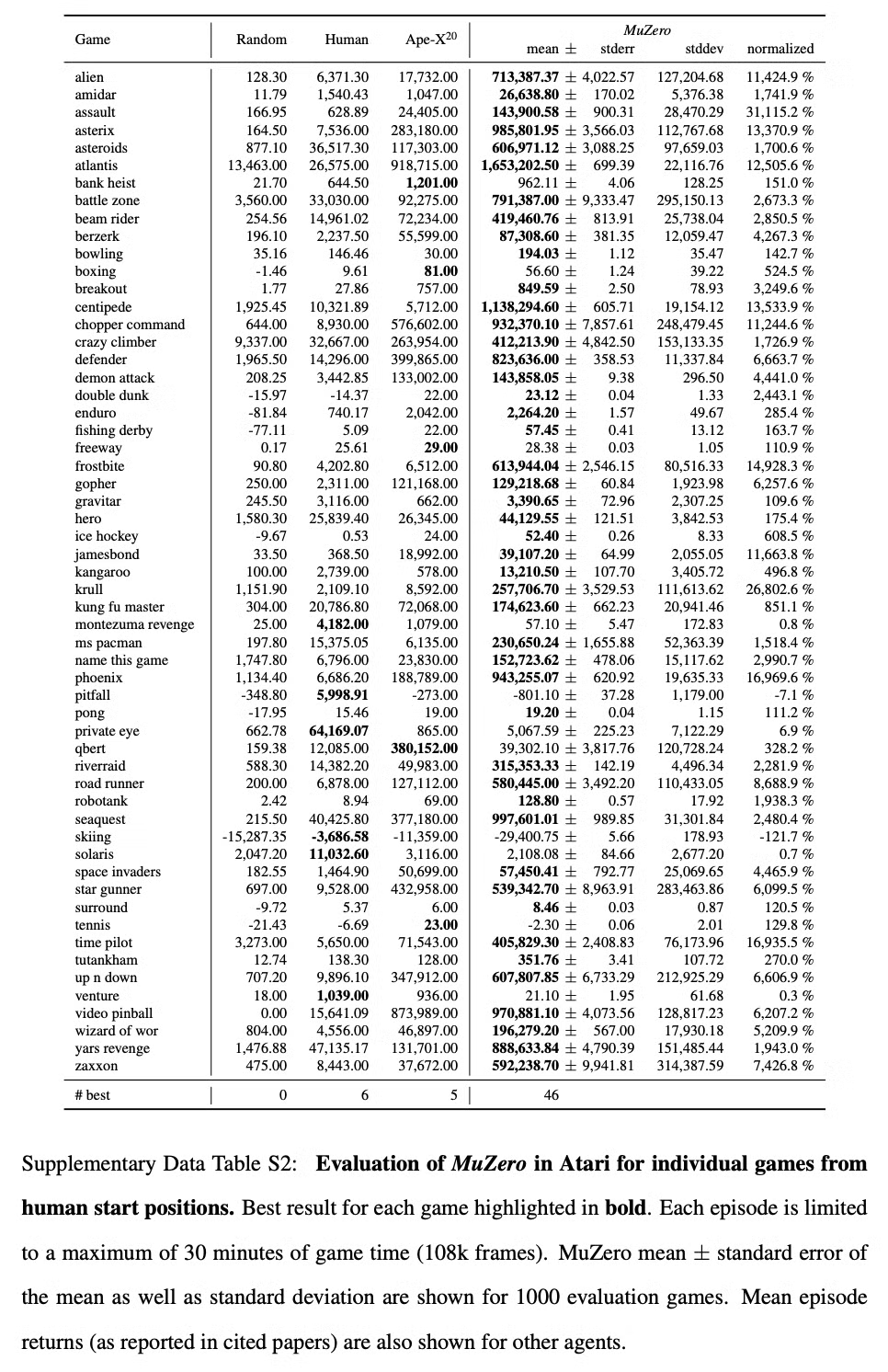
- Atari simulator의 deterministic nature 효과를 피하기 위해 두개의 다른 평가 전략 사용
- 30 noop random start
- human start
- 전자의 경우 매 에피소드의 시작에 에이전트가 제어하기 전 0부터 30 사이의 랜덤한 수 동안 noop action을 적용
- 후자의 경우 에이전트가 제어하기 전 사람이 Atari simulator를 플레이하고 이를 초가화하여 시작 위치 샘플링
Supplymentary
Fig. S1
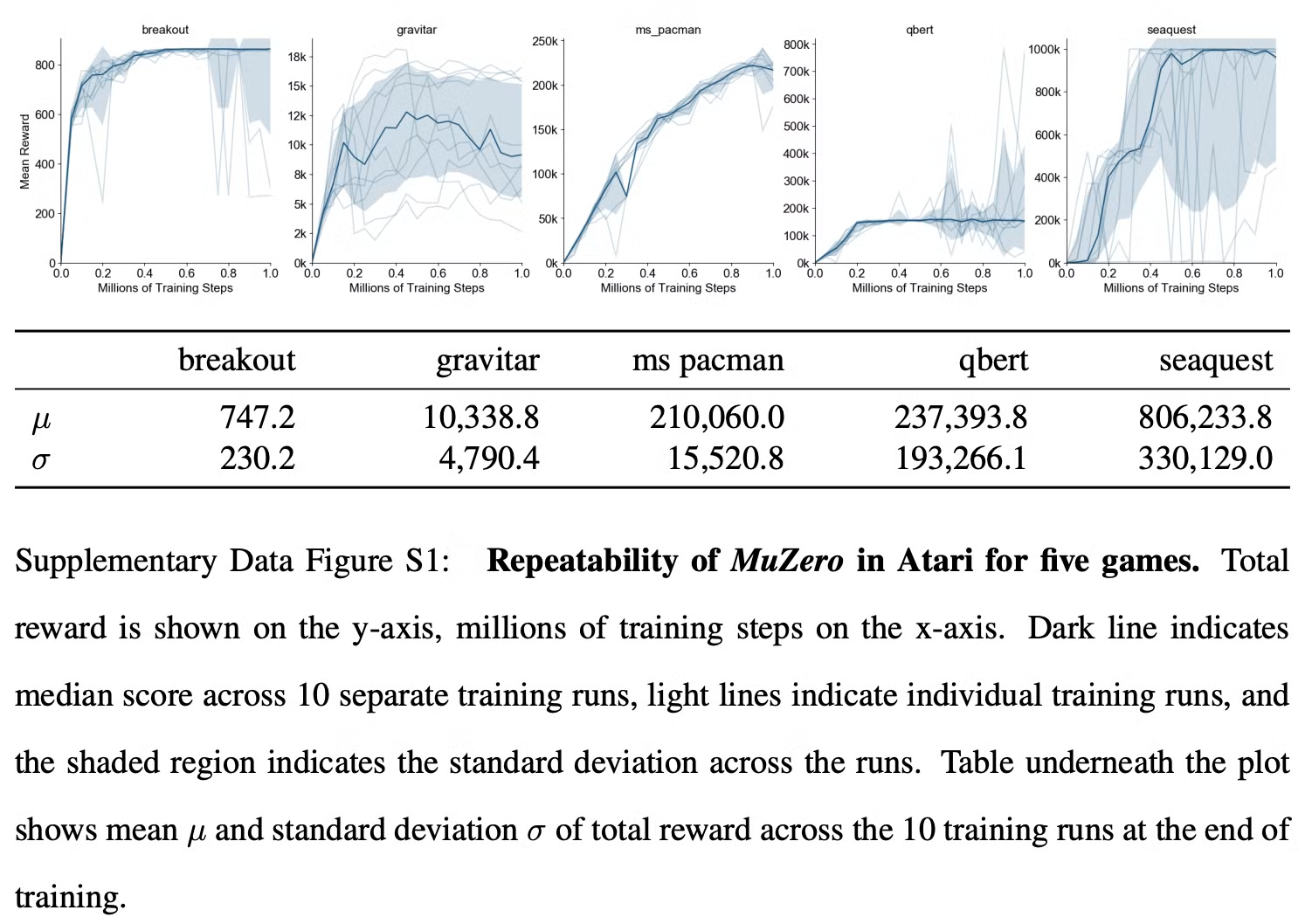
Fig. S2

Fig.S3
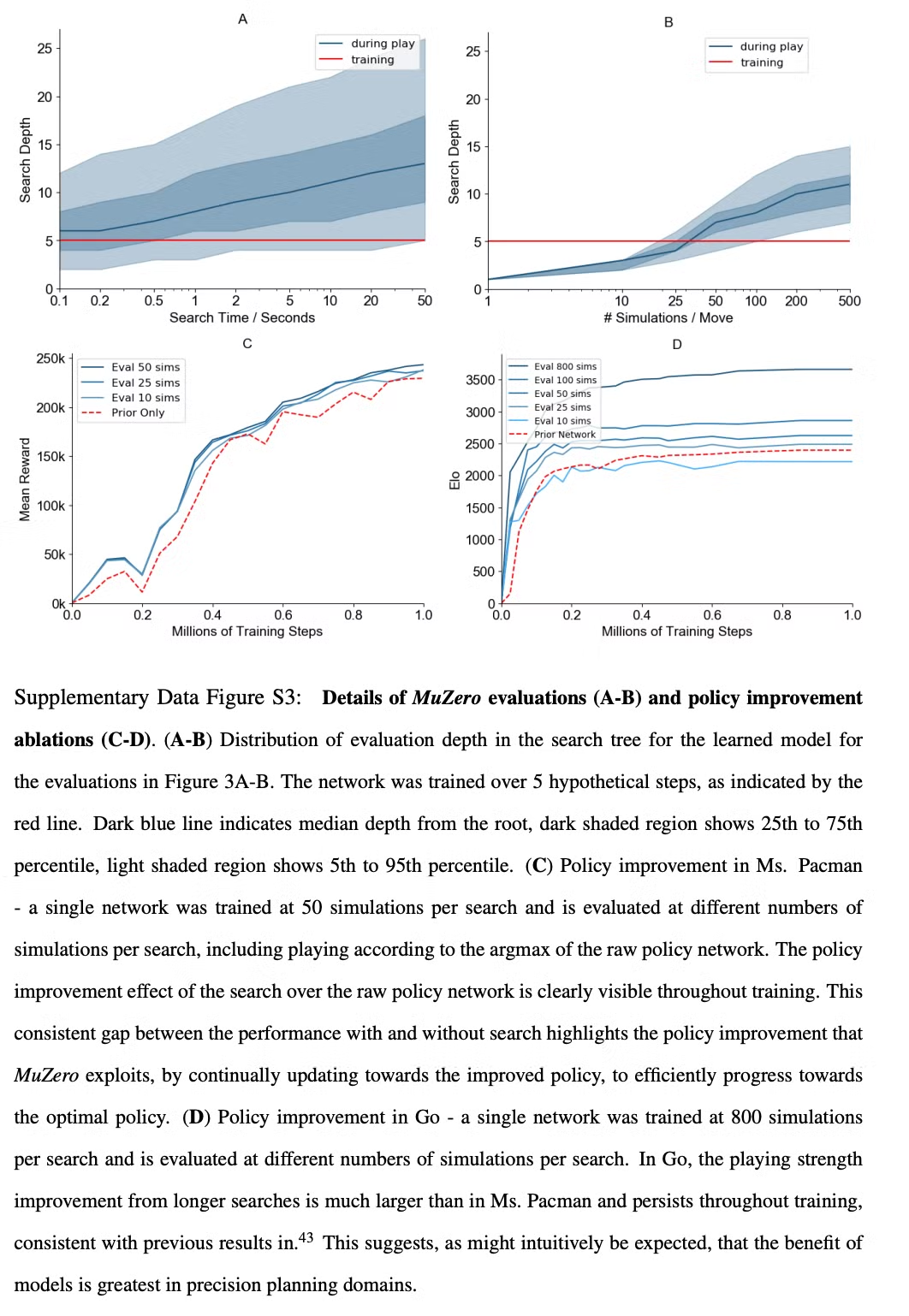
Fig S4
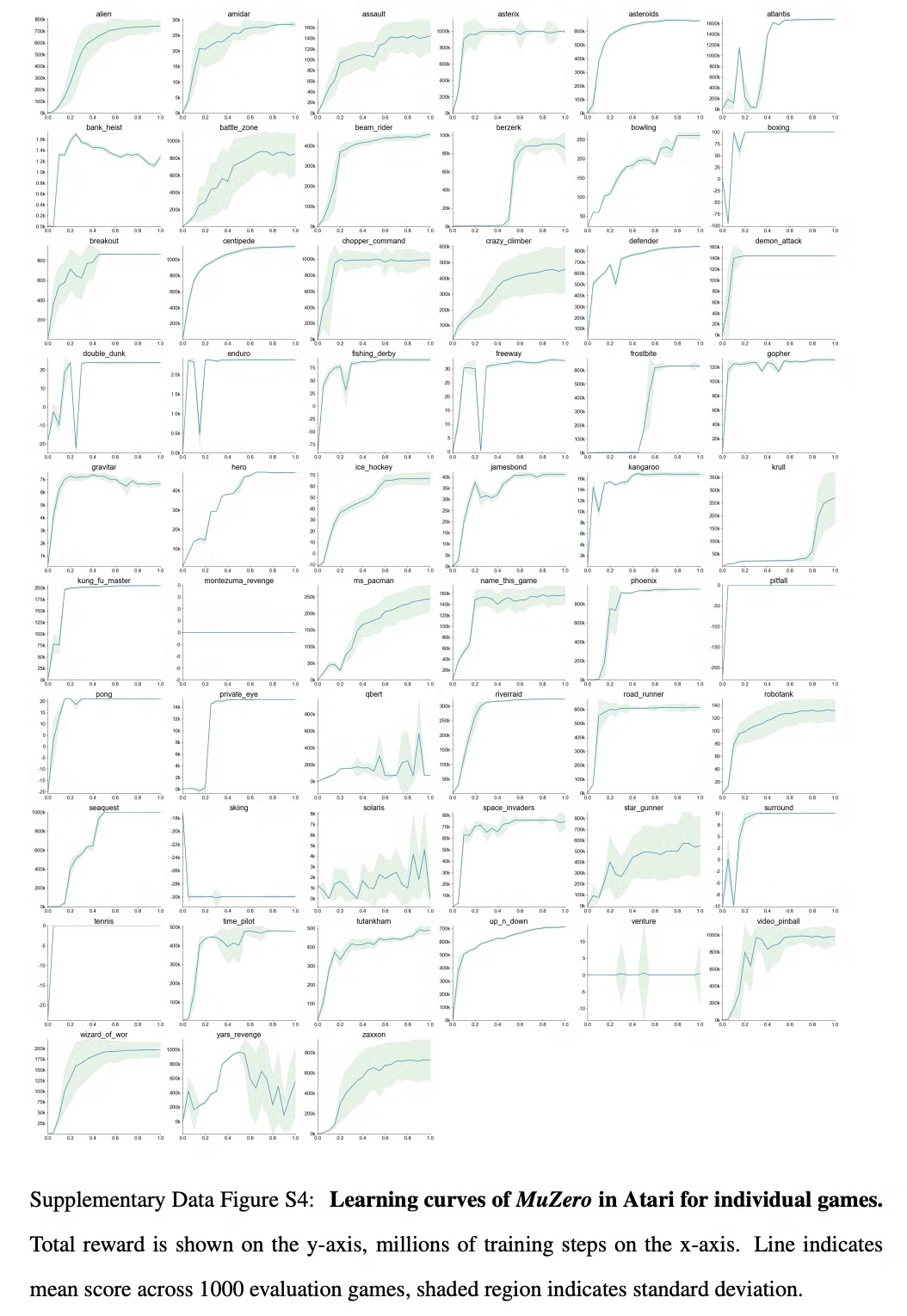
Fig. S5
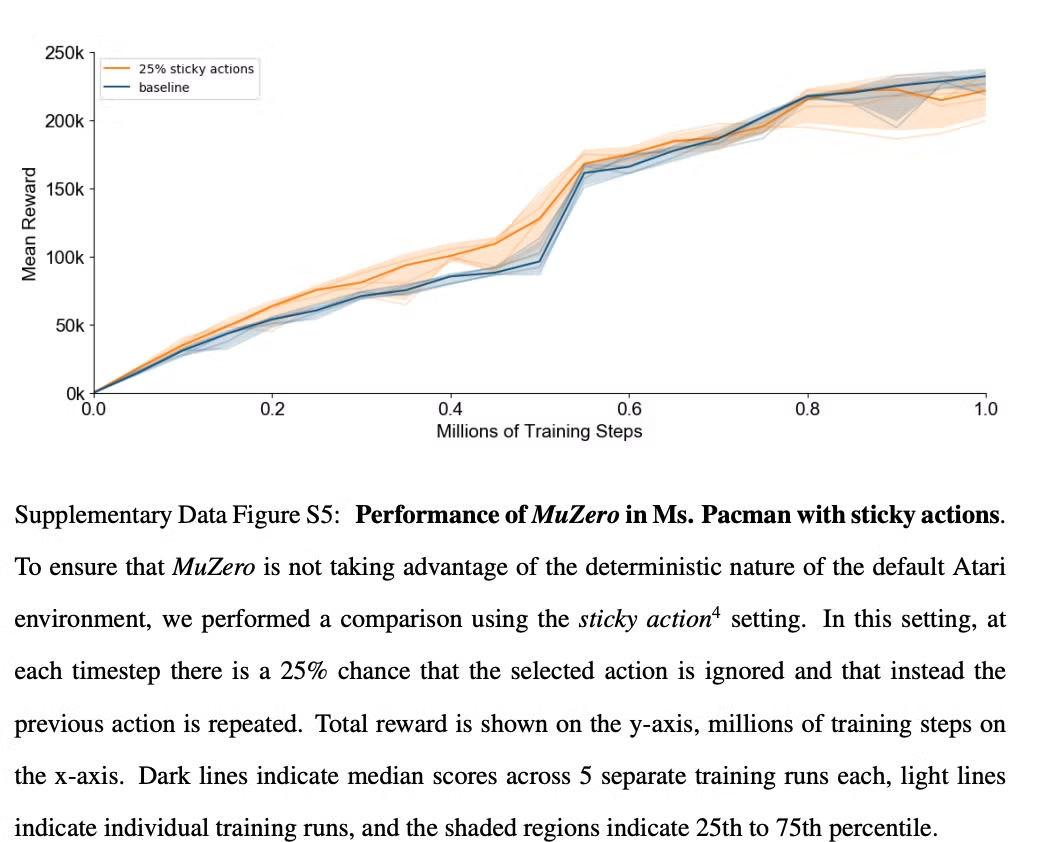
Table S1
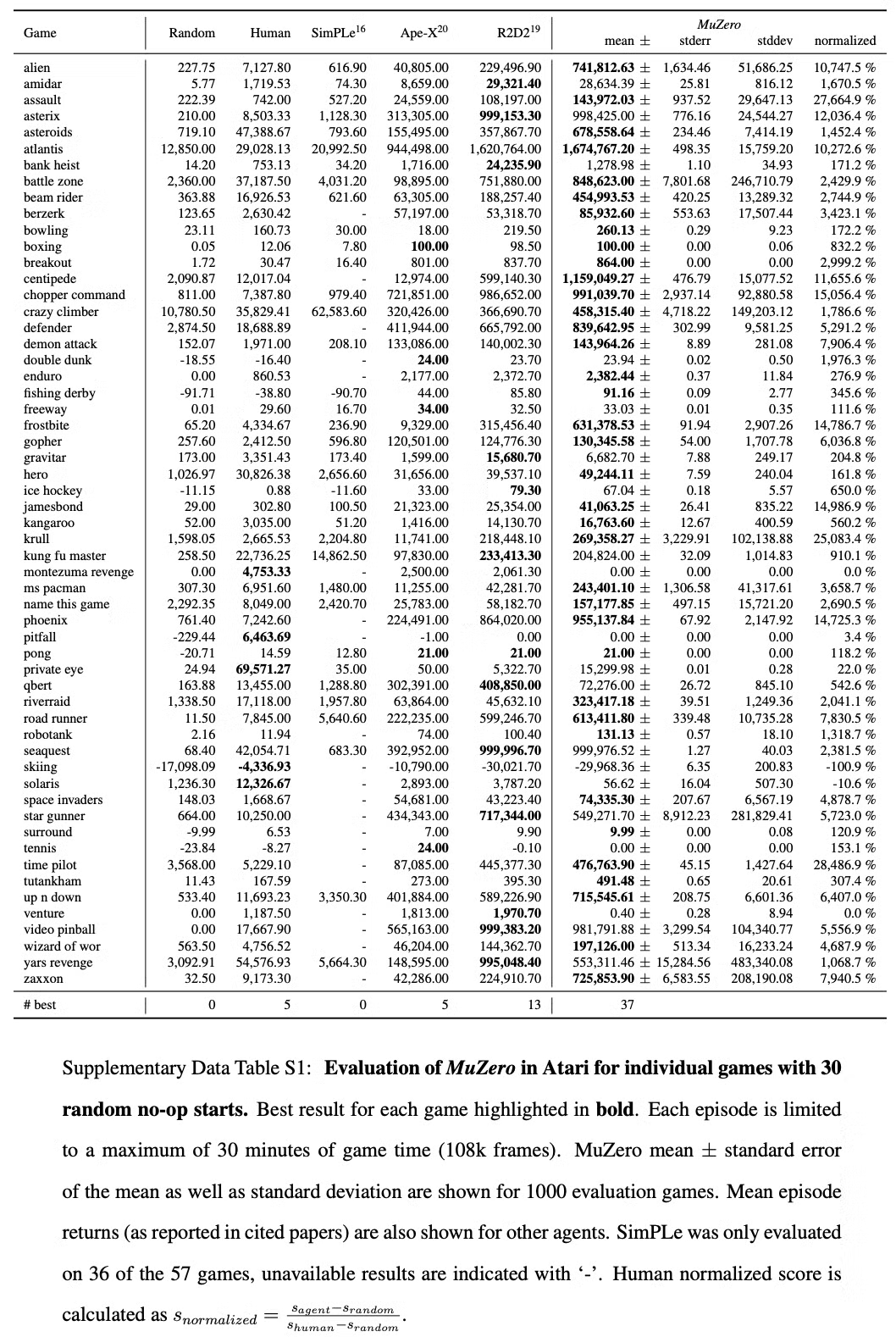
Table S2
'논문 리뷰 > Reinforcement Learning' 카테고리의 다른 글
| Estimating Risk and Uncertainty in Deep Reinforcement Learning (0) | 2024.11.03 |
|---|---|
| [Sampled MuZero] Learning and Planning in Complex Action Spaces (0) | 2024.10.15 |
| [M-RL] Munchausen Reinforcement Learning (1) | 2024.09.16 |
| [RND] Exploration by Random Network Distillation (1) | 2024.09.13 |
| [RND] Exploration by Random Network Distillation (5) | 2024.09.11 |



