Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction (BEAR)

논문 링크: https://arxiv.org/pdf/1906.00949.pdf

 

0. Abstract

• 기존의 강화학습 기법을 적용하는 경우 추가적인 on-policy data 수집 없이는 성능이 제한적
• 제안하는 문제 세팅: off policy 경험을 고정하고 환경과 상호작용이 없도록
  • 현재 instability의 주요 요소 → Bootstrapping error
  • 학습 데이터의 분포 바깥에 있는 데이터의 행동에 의해 boostrapping error 발생
  • Bellman backup operator에 의해 누적
• 제안하는 기법: Bootstrapping Error Accumulation Reduction (BEAR)
  • 행동 선택에 제한을 두어 backup이 이를 피할 수 있도록 함

1. Introduction

• 기존 강화학습의 한계
  • 대부분의 강화학습 알고리즘은 active data collection을 요구하기 때문에 unstructured real world 세팅에 확장하여 적용하기 어려움
  • 결과적으로 RL 알고리즘은 직관적으로 데이터 수집이 가능한 시뮬레이션에서는 복잡한 행동에 대한 학습을 할 수 있지만 activate data collection이 어렵다는 이유로 real world에서는 성능이 제한적
• Off-policy RL
  • Off policy RL을 이용하면 수집된 데이터에 대한 학습이 가능
  • Off policy 데이터가 환경과 상호작용을 통한 추가적인 데이터 수집의 기회가 없으면 여전히 학습이 실패
  • training data 분포에 대한 sensitivity도 off-policy RL 알고리즘의 실용적 적용을 제한적으로 만드는 요소
  • 이에 따라 실제 적용 전에 static dataset으로 부터 reasonable policies를 학습할 수 있는 방법 필요
• 본 논문의 제안-
  • Large, static dataset으로부터 학습하는 off-policy value-based RL 기법 제안
  • Value based 기법을 off-policy 시나리오에 적용할 때 가장 주요한 challenge
    • Bootstrapping 과정에서 backup을 수행할 때 Q-function이 out-of-distribution 행동 입력으로 평가되는 경우 문제 발생
    • 이 과정에서 Q-function에 에러가 발생하고 알고리즘은 이 에러를 해결할 수 있는 새로운 데이터를 얻을 수 없음 → 학습이 불안정해짐
  • 본 논문의 주요 contribution
    • Out-of-distribution 입력에 의해 발생하는 boostrapping 과정에서의 error accumulation과 해당 에러를 해결할 수 있는 실용적인 방법에 대해 분석
    • Off policy Data를 통해 학습했을 때 불안정성과 성능 감소에 대한 이유 분석
    • Careful action selection을 통해 Q-function에서 에러가 전파되는 것을 피할 수 있다는 것을 보여줌
  • 제안하는 알고리즘 → Bootstrapping Error Accumulation Reduction (BEAR)
    • Support-set matching의 개념을 사용하여 error accumulation 방지

2. Related Work

• Motivation
  • Inadequate sampling, distributional shift, function approximation 등이 Approximate Dynamics Programming (ADP)에서 "error propagation"으로 연구되고 있음
  • 어떻게 bellman error가 누적되고 bootstrapping을 통해서 주변의 상태들로 전파되는지 연구
  • 본 논문에서는 static datasets에서 Bellman backups를 수행할 때 어떻게 out-of-distribution value가 error accumulation으로 이끄는지 살펴봄
  • 본 논문의 motivation → 상태들 사이에서 error propagation
• Batch-constrained Q-learning (BCQ)와의 비교
  • BEAR가 BCQ보다 나은 점 → sub optimal이나 random하게 수집된 데이터에서 좋은 성능을 보임 (real life application을 통해 얻을 수 있는 데이터의 특징과 유사)

3. Background

• Markov Decision Process (MDP): $(S, A, P, R, \rho_0, \gamma)$
• Bellman optimality operator에 기반한 Q-learning algorithm
  

  

4. Out-of-Distribution Action in Q-Learning

• Q-learning 기법은 Figure 1과 같이 static, off-policy 데이터에서의 학습 실패
• 얼핏 보기로는 overfitting과 유사하지만 static dataset의 사이즈를 늘리는 것 만으로 문제가 해결되지 않음
• 본 논문에서는 이 문제를 Bellman backup 때문에 발생하는 것으로 생각
• Bootstrapping Error
  • Mean squared Bellman error를 최소화하는 것은 supervised regression 문제와 유사해보이지만 이 regression의 target은 현재 Q-function의 추정을 통해 얻어짐
  • Target은 다음 상태에서 행동에 대한 학습된 Q-value를 최대화하도록 계산
  • 그러나 Q-function estimator는 학습 셋과 동일한 입력에 대해서만 reliable
  • 결과적으로 training distribution으로부터 멀리 떨어진 action을 이용하여 단순히 Q estimator를 평가하는 것은 큰 에러를 유발할 수 있음 → out-of-distribution (OOD) action
• Bellman Backup Operator
  • Q-learning의 iteration $k$에서 total error
    

    

  • 현재 Bellman error
    

    

  • 위를 통해 다음과 같이 정의 가능
    

    

  • 즉 $(s',a')$에 의한 에러가 감가되고 현재 iteration에서 새로운 에러 $\delta_k (s,a)$에 누적됨
  • 우리는 $\delta_k(s,a)$가 OOD state와 actions에서 높을 것으로 예상 → 이런 상태와 행동에 대한 에러는 학습중에 직접적으로 최소화 될 수 없음
• Bootstrapping Error를 피하는 방법
  • Policy의 output action이 training distribution의 support 내에 있어야 함
  • 이는 BCQ에서 사용한 방식과 유사 → 학습된 policy의 distribution을 behavior policy와 유사하도록 제한
  • 이는 action이 training set 내에 높은 확률로 있을 것으로 보장 → 너무 restrictive
  • 만약 behavior policy가 uniform에 가까우면 만약 데이터가 충분히 좋은 policy를 학습할 수 있는 경우에도 학습된 policy는 랜덤하게 행동하고 나쁜 성능을 보임
• 본 논문의 기법
  • "Data distribution 내에 있는 것"과 "constraint가 너무 제한적일 때 sub optimal solution을 찾는 것" 사이의 trade off를 분석
  • 학습된 policy의 support를 제한하지만 support 내 action의 확률을 제한하지는 않음
  • Q-function estimator가 OOD action에서 evaluate하는 것은 피하지만 performant policy를 찾을 수 있도록 flexibility는 남겨놓음

4.1 Distribution-Constrained Backups

• Q-function의 최대화에 사용하는 set of policies를 제한하는 backup operator 정의 및 분석
• 제한된 set에 의존하는 performance bound 도출 → 데이터 분포에 대한 policy support를 제한하는 motivation
• Distribution-constrained operators
  

  

  • Backup operator는 표준 Bellman equation의 특성을 만족
  • Approximation error 하에서 이 backup 수행의 (sub)optimality를 분석하기 위해 에러의 2가지 source를 quantify
    1. Suboptimality bias → optimal policy가 policy constraint set의 밖에 있는 경우 suboptimal solution을 찾음
    2. Training distribution과 backup에 사용하는 policies 사이의 distribution shift로부터 발생
• 최종 solution의 suboptimality를 알아내기 위해 suboptimality constant를 정의
  

  

  • 얼마나 $\pi ^*$가 $\Pi$와 차이가 있는지 측정
• Concentrability coefficient를 정의 → $\Pi$의 policies에 의해 생성된 visitation distribution이 얼마나 training data distribution과 차이나는지 수량화
  

  

  • 이 상수는 상태와 행동의 OOD 정도를 알려줌
  • $C(\Pi)$에 대한 직관적인 설명
    • 만약 $\mu$가 single policy $\pi$에 의해 생성되면 $\Pi=\{\pi\}$가 singleton set이고 $C(\Pi)=1$ → 가능한 수 중 가장 작음
    • 만약 $\Pi$ constrained policies가 $\pi$와 차이가 많으면 이 값은 커지게 되고 $\Pi$의 support가 $\pi$에 포함되어있지 않으면 무한해질수도 있음

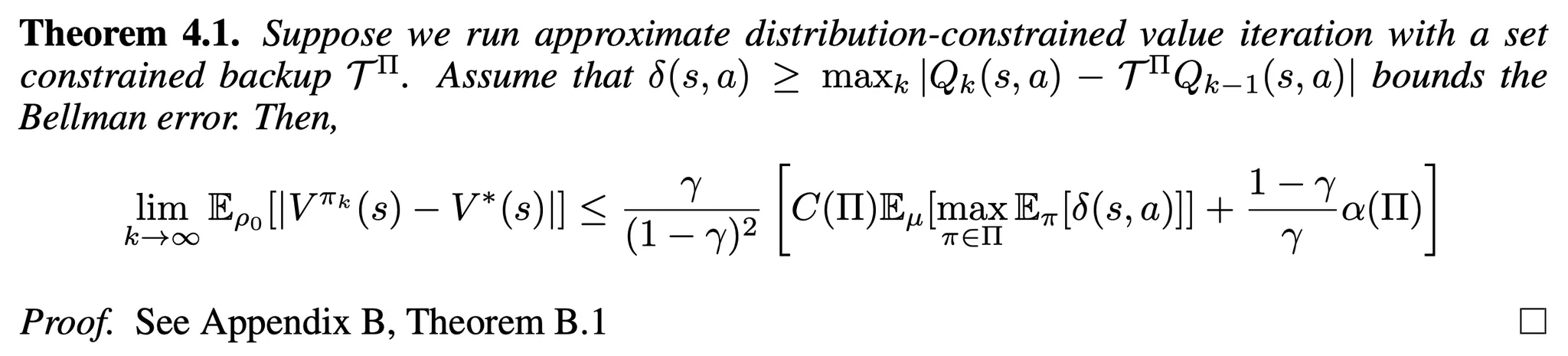
• 이 bound는 "backup 동안 policies를 data와 유사하게 유지하는 것"과 "$\Pi$를 충분히 크게하여 잘 동작하는 policies를 찾는 것" 사이의 trade off를 수식화한 것
  • set of policies $\Pi$를 확장하면 $C(\Pi)$는 커지고 $\alpha(\Pi)$는 감소
  • Figure 2 → 이 trade off의 예시와 어떻게 careful choice of $\Pi$가 superior result를 만들 수 있는지 보여줌
    

    

• 마지막으로 $\Pi$를 construct 하기 위해 support set을 사용하는 것에 대한 motivate
  • 관심있는 상황 → $\Pi_{\epsilon}=\{\pi|\pi(a|s)=0 \ whereever \ \beta(a|s)<\epsilon \}$ ($\beta$: behavior policy)
  • $\Pi_{\epsilon}$ 을 이렇게 설정하면 concentrability coefficient를 제한할 수 있음 (Data distribution $\mu$가 behavior policy $\beta$에 의해 생성되는 경우)
    

    

    • Training action distribution의 support에 의해 supported된 selecting policy에 의한 Q-estimate의 overall error 증가 방지

5. Bootstrapping Error Accumulation Reduction (BEAR)

• Practical actor-critic 알고리즘 (TD3나 SAC의 프레임워크로 개발)에 distribution-constrained backups를 사용 → bootstrapping error의 누적을 감소
• accidental error accumulation은 방지하면서 학습 distribution과 동일한 support를 가지는 policy를 찾을 수 있음
• 제안된 알고리즘은 2가지 요소를 가지고 있음
  1. K개의 Q-function을 사용하고 이들 중 최소값을 policy improvement에 사용, 최소값이 아니라 평균값을 써도 괜찮은 성능 도출
  2. set of policies $\Pi_{\epsilon}$을 searching하기 위해 사용하는 constraint를 디자인 → behaviour policy와 동일한 support를 공유
• 위의 두 요소 모두 actor-critic 스타일 알고리즘에서 policy improvement step를 변경한 것
• 기법1: K 개의 Q-function 사용
  • Q functions의 set을 $\hat{Q}_1, ..., \hat{Q}_K$로 정의
  • policy는 $\Pi_{\epsilon}$ 내에서 Q-value의 conservative estimate를 maximize 하도록 업데이트
    

    

• 기법2: Constraint
  • Behaviour policy $\beta$가 unknown인 경우 $\Pi$를 $\pi$로 제한하기 위해 근사적인 방법 필요
  • $\pi$를 $\Pi$로 근사하기 위해 미분 가능한 constraint를 정의하고 dual gradient descent를 통해 constrained optimization problem을 근사적으로 풀어줌
  • 본 논문에서는 unknown behaviour policy $\beta$와 actor $\pi$ 사이의 Maximum Mean Discrepancy (MMD)의 sampled version 사용 → Distribution으로부터의 샘플만에 의존하여 추정 가능
  • 주어진 sample이 $x_1, ..., x_n \sim P$와 $y_1, ..., y_m \sim Q$ 일때 P와 Q 사이의 sampled MMD는 다음과 같음
    

    

• 위 내용들을 종합한 policy improvement step의 optimization problem
  

  

  • $\epsilon$: approximately chosen threshold → 논문의 실험에서는 0.05로 설정
• 알고리즘
  

  

• 요약
  • actor는 Q-function을 maximize하는 방향으로 업데이트되면서도 여전히 $\Pi_{\epsilon}$에 의해 정의된 valid search space에 남아있도록 제한
  • Q-function은 actor에 의해 samping된 action을 사용 → reduced set of policies에서 distribution-constrained Q-learning 수행

6. Experiments

• Static off-policy data를 continuous control benchmark test에서 사용
• 세가지 세팅의 policy를 통해 수집한 데이터를 통해 검증
  1. 완전 random behaviour policy
  2. partially trained, medium scoring policy
  3. optimal policy
• 성능 비교 알고리즘
  • baseline actor-critic algorithm (TD3)
  • BCQ
  • KL-control
  • DQfD
  • Behavioral Cloning (BC)

6.1 Performance of Medium-Quality Data

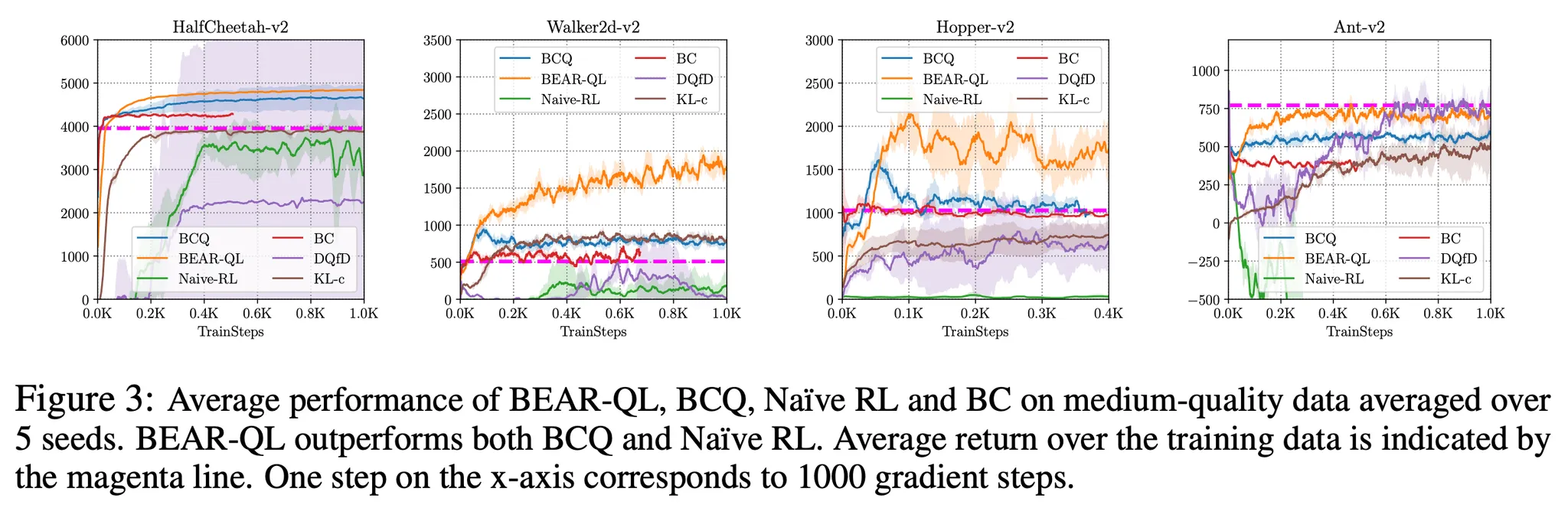
• 적당한 퀄리티의 데이터를 이용한 성능 검증 → partially trained policy를 통해 수집된 100만 transition 데이터
• Figure 3의 결과를 통해 BEAR-QL이 BCQ나 naive off-policy RL baseline (TD3)의 성능에 비해 크게 향상된 성능을 보임

6.2 Performance on Random and Optimal Datasets

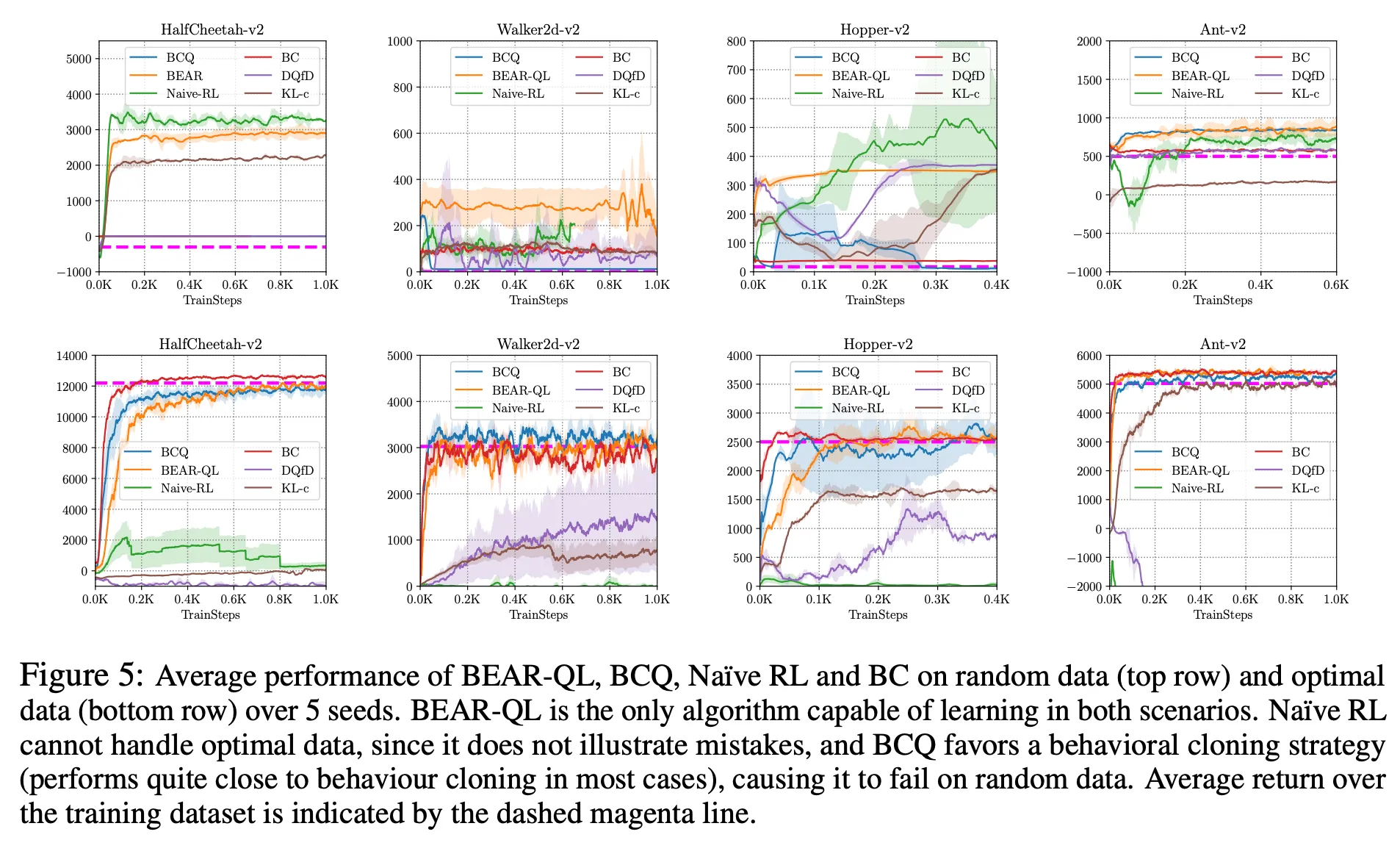
• Figure 5는 각 기법에서 random policy (top)와 near-optimal policy (bottom)에 의해 수집된 데이터로 학습한 결과를 보여줌
• 이 경우에도 BEAR가 좋은 성능을 보임
  • random data에서도 평균 dataset return을 꾸준히 넘는 성능
  • optimal data에서도 optimal policy와 유사한 성능
• BCQ의 경우 optimal data에서는 잘하지만 random data에서는 나쁜 성능 → constraint가 너무 strict
• Figure 4를 살펴보면 BEAR가 어려운 Humanoid-v2에서도 Medium quality data, random data에서 좋은 성능을 보이는 것 확인
  

  

6.3 Analysis of BEAR-QL

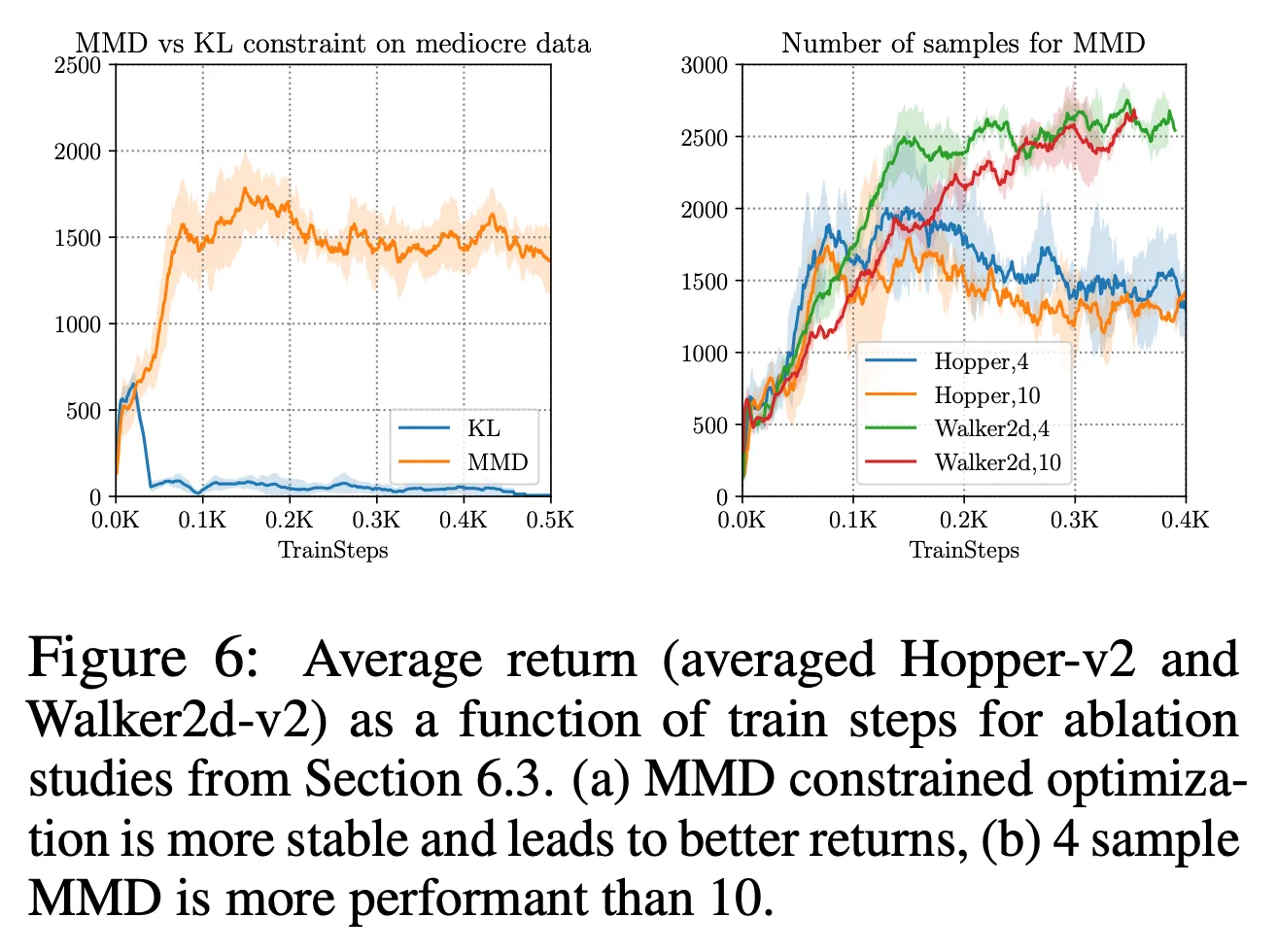
• 2가지 ablation study 진행
  1. support constraint를 MMD → KL-divergence distribution constraint
     • 더 conservative한 constraint 제공
     • optimal data와 같은 어떤 케이스에서는 좋은 성능을 보였으나 Figure 6에서처럼 medium-quality data에서는 MMD에 비해 나쁜 성능을 보임
  2. MMD constraint를 계산할 때 샘플의 수 $n$을 다양화
     • 더 작은 $n$ ($\approx$ 4 or 5)가 더 좋은 성능을 보임

7. Discussion and Future work

• 본 논문의 목표: static dataset에서 off-policy reinforcement learning 적용
• 이론적, 경험적으로 Bellman backup에서 target value 계산시 out-of-distribution action의 사용이 off-policy RL에서 어떻게 에러를 전파시키는지 분석
• OOD action의 영향을 피하는 방법에 대한 연구 수행 → BEAR-QL
• BEAR-QL은 data distribution 하에서 non-negligible support를 가지는 행동을 사용하여 backup을 제한하면서도 학습 policy을 너무 엄격하게 제한하지는 않음
• BEAR-QL이 다양한 환경에서 좋은 성능을 보임 → 다양한 데이터셋 구성 (random, medium-quality, expert data)
• 본 논문의 limitation
  • long learning runs를 수행하면 성능 감소 발생 → future work: early stopping condition
  • constrained-action selection 기반의 접근 → state-distribution을 직접적으로 제한하는 방법과 비교했을 때 너무 conservative
• Future work
  • BEAR-Q을 large-scale off-policy learning problem에 적용하는 것 → robotics, autonomous driving, operations research, commerce