Paper link: https://arxiv.org/pdf/1812.02900.pdf
BCQ 구현 관련 사항
- 총 4가지 모델 사용
- Generative model: $G_{\omega}(s)$
- Perturbation model: $\xi_{\phi}(s,a)$
- Q-networks: $Q_{\theta_1}, Q_{\theta_2}$
- Algorithm

Generator
- Encoder $E_{\omega_1}(s,a)$와 Decoder $D_{\omega_2}(s,a)$로 구성 → VAE
- Encoder는 $\mu, \sigma$를 도출 → z를 sampling → Decoder의 입력으로 s, z 사용 → action을 예측
- 학습은 예측 action과 실제 action이 유사하도록, KL divergence를 통해 mu=0, sig=1이 되도록 학습
- Generator를 통해 n개의 action 도출
Perturbation Network
- Generator가 도출한 action에 noise 추가 → $\{a_i = a_i + \xi_{\phi}(s',a_i,\Phi)\}$
- Perturbation이 추가된 action의 Q가 최대가 되도록 학습
- $\phi \leftarrow argmax_{\phi}\sum{Q_{\theta_1}(s,a+\xi_{\phi}(s,a,\Phi))}, a \sim G_{\omega}(s)$
- Perturbation network의 경우 target network 사용 (soft update)
- $\phi' \leftarrow \tau \phi + (1-\tau)\phi$
Q-Network
- 일반 Q value 학습과 동일
- $\theta \leftarrow argmin_{\theta} \sum(y-Q_{\theta}(s,a))^2$
- Q-network도 target network 사용 (soft update)
- $\theta_i' \leftarrow \tau \theta + (1-\tau) \theta_i'$
내용 정리









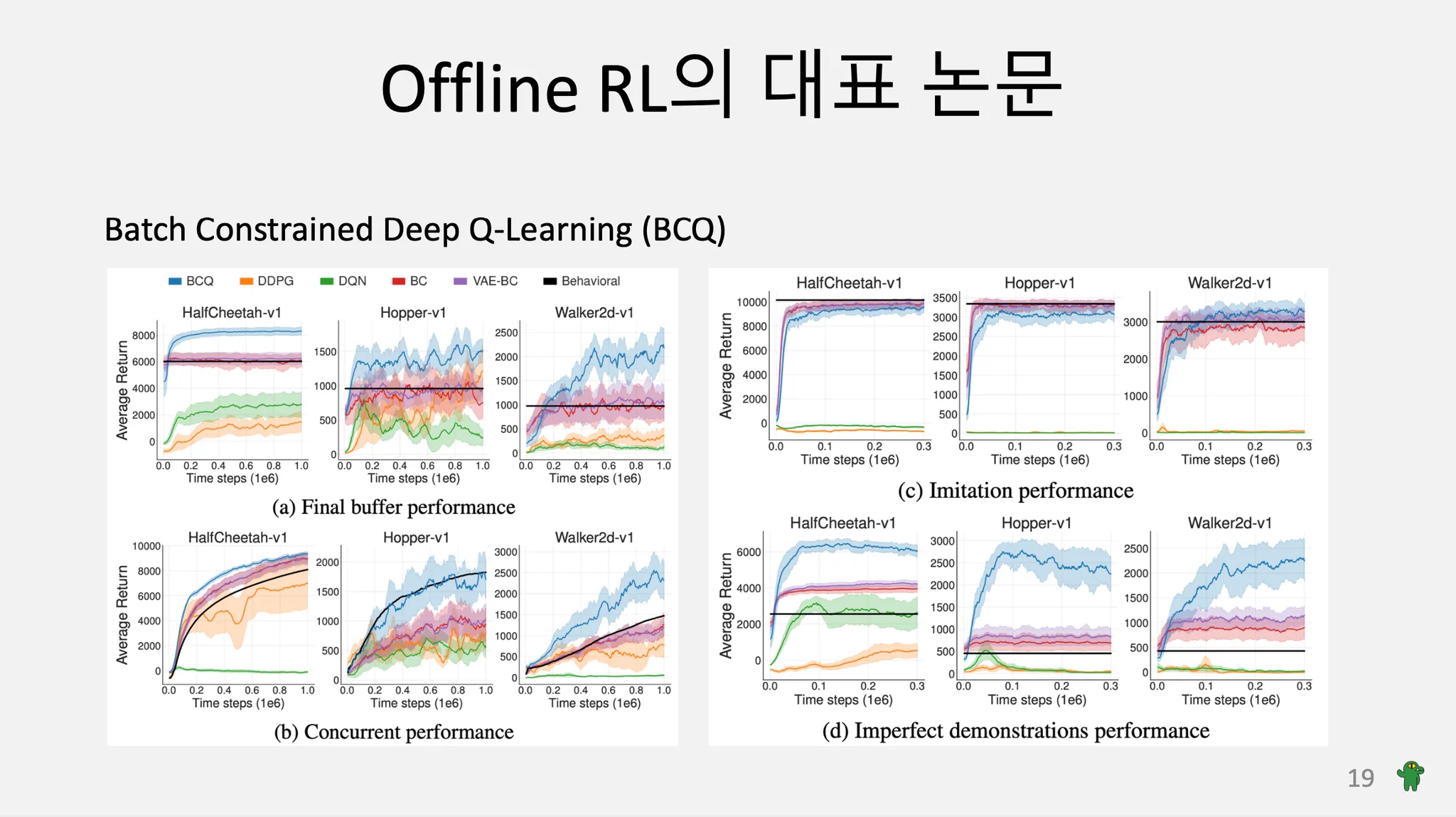
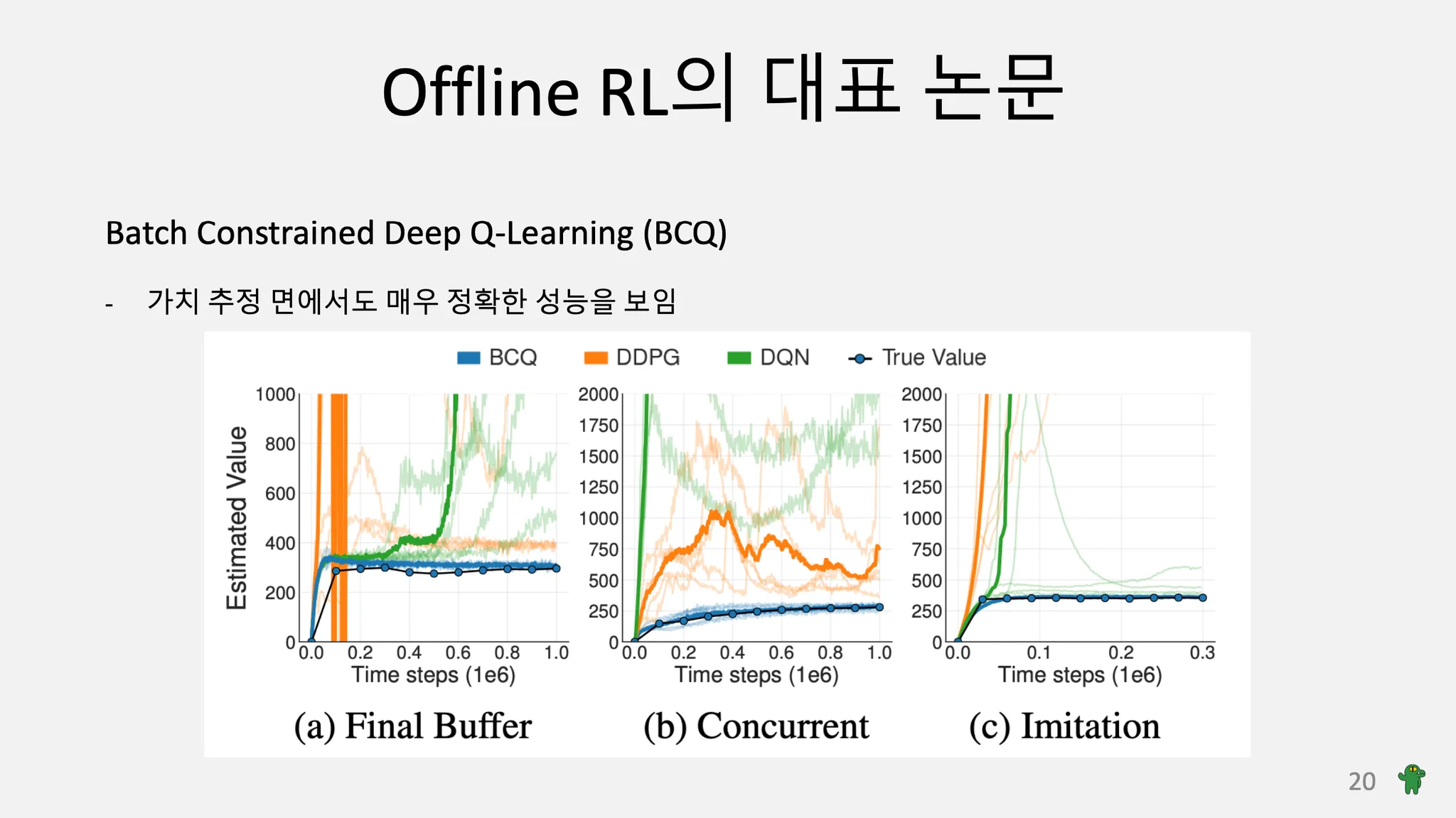
'논문 리뷰 > Offline RL' 카테고리의 다른 글
| Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction (BEAR) (1) | 2024.11.27 |
|---|---|
| Understanding the World Through Action (0) | 2024.11.25 |

