반응형

0. Abstract
- Program Synthesis는 주어진 입출력 쌍에 대해 이를 설명할 수 있는 프로그램을 자동으로 생성하는 문제
- 기존 접근 방식
- 기호 기반 (symbolic) 접근
- 조합 탐색 공간 (combinatorial search space)이 커지는 경우 풀기 어려움
- 인공 신경망 기반 접근
- 인공신경망을 사용하여 프로그램 구조에 대한 분포를 학습하고 탐색 공간을 줄여 효율성을 향상시킴
- 하지만 어려운 문제에 대해서는 한번에 (one-shot) 프로그램 합성을 하는 것이 어려움 → test-time search가 추가적으로 필요
- 하지만 대부분의 신경망 기반 접근은 추론 동안 구조적 검색을 하지 않고 확률적 샘플링이나 기울기 (gradient) 업데이트에만 의존 → 비효율적
- 기호 기반 (symbolic) 접근
- 본 논문에서는 LPN (Latent Program Network)을 제안
- 연속적인 공간에서 잠재 프로그램의 분포를 학습하는 일반적인 프로그램 추론 알고리즘 → 효율적인 탐색과 test-time adaptation 가능
- 본 논문에서는 test-time computation을 최적화하며 학습과 테스트 시점 모두에서 기울기 기반 탐색을 사용하는 네트워크 학습 방법을 제안
- 평가
- LPN을 ARC-AGI에서 평가 수행
- ARC-AGI: Program synthesis 벤치마크로 새로운 입력에 대해 프로그램을 일반화하는 성능을 평가
- 본 논문에서는 test-time computation을 통해 LPN이 학습 분포를 넘어 본적 없은 문제도 적응하도록 함
- LPN을 ARC-AGI에서 평가 수행
1. Introduction
- Program Synthesis: 주어진 입출력 예시를 만족하는 프로그램을 자동으로 생성하는 과제
- 기존 접근 1: 기호 기반 (Symbolic) 접근
- 제한된 문제에서는 효과적이나 ARC-AGI와 같이 큰 탐색 공간과 복잡한 패턴을 가지는 문제에 대해서는 확장성 부족
- 기존 접근 2: 신경망 기반 (Neural) 접근
- 데이터를 기반으로 프로그램 탐색의 범위를 줄이도록 학습
- 최근에는 LLM이 program synthesis 문제를 해결하기 위한 강력한 구조로 떠오름
- 장점
- 이미 많은 텍스트와 코드로 사전학습 되어있어서 사전 지식을 가지고 있음 → 탐색 공간이 줄어들어 효율적인 program synthesis 가능 → 이는 ARC-AGI와 같이 데이터가 적은 경우 유용함
- 단점
- 이런 모델은 특정한 프로그램 분포에 대해서는 일반화되어 있으므로 ARC-AGI와 같이 분포를 벗어나도록 (Out-of-distribution) 특별히 디자인 된 문제에 대해서는 낮은 성능을 보임
- 테스트 시 탐색을 수행하지 않음
- 파인튜닝을 하는 경우 계산 비용이 많이 들어가고 높은 오버피팅 가능성이 있음
- 장점
- 위와 같은 기존 접근들의 한계를 극복하기 위해 일반적이면서도 확장 가능한 알고리즘인 **Latent Program Network (LPN)**을 제안
- 인공신경망 구조에 직접적으로 test-time adaptation을 적용 → test-time search를 위한 학습 목적 함수를 사용 → test-time adaptation을 통한 일반화 수행
- 넓은 범위의 프로그램에 대한 연속적인 잠재 공간을 사용
- 학습과 추론 시 구조화된 잠재 공간에서 탐색 능력을 가짐 → 테스트 시점에서 효율적인 적응이 가능하도록 함
- 잠재 공간에서 기울기 기반 최적화를 수행 → 새로운 입력에 대해 대응하는 출력을 생성하는 잠재 프로그램
- 디코더가 특정 입력에 대해 픽셀 단위로 출력을 직접 생성
- LLM과 같은 대형 모델과 대비되도록 처음부터 인공신경망을 학습
- 또한 사람이나 LLM이 생성한 추가 합성 데이터를 사용하지 않음 → 오직 re-arc 데이터만의 입력-출력 쌍을 학습 데이터로 사용
- 본 논문의 주요한 기여점 (Main Contribution)
- LPN (Latent Program Network)을 제안
- 가능한 프로그램의 공간을 나타내는 잠재 공간을 학습하여 test time adaptation이 가능한 구조 설계 → 잠재 공간을 움직이며 출력 디코더의 test-time adaptation이 가능하도록 함
- 출력이 직접적으로 잠재 공간에 인코딩 되지 않도록 잠재 공간을 학습하는 학습 목적 함수를 사용
- 입력-출력 쌍을 잠재 공간에 인코딩하지만 이것들이 다른 입력-출력 쌍의 출력으로 디코딩 되도록 학습
- 잠재 공간이 프로그램 공간 대신 출력 공간을 나타내는 것을 방지
- 잠재 공간에서 기울기 기반 탐색을 수행
- 잠재 탐색을 적용하지 않을 때의 성능과 비교했을 때 LPN의 성능을 크게 향상시킴
- 학습 동안 기울기 기반 잠재 탐색을 추가
- 잠재 공간에서 잘 동작하는 기울기 최적화 학습 수행 → 샘플 효율성을 크게 향상시킴
- 사전 학습 모델 / LLM / 사람이 생성한 합성 데이터를 사용하지 않음
- re-arc 데이터의 입력-출력 쌍을 사용하여 학습
- 또한 현재 결과는 충분히 수렴하지 않은 결과 → 연산량과 파라미터의 확장으로 ARC-AGI의 성능을 더욱 향상시킬 수 있음
- 기존 연구에서 주장한 vision transformer가 arc 의 단일 문제도 학습하기 어렵다는 내용을 반박 → 본 논문은 순수하게 픽셀 단위로 출력을 예측하는 신경망 기반 접근으로도 ARC-AGI를 해결할 수 있음을 보임
- LPN (Latent Program Network)을 제안
2. Background
Program Synthesis
- Program Synthesis의 목표: 주어진 specification과 규칙과 일치하도록 입력이 들어왔을 때 타겟 언어로 출력을 생성하는 결정적 프로그램 (deterministic program)을 생성
- 여기서 problem space $Y$는 특정 도메인의 언어 (Domain-specific Language, DSL)로 수식화 된 프로그램으로 구성됨
- 각 문제 (task)는 specification의 세트 $X$로 정의 → 각 specification $X_m \in X$는 입/출력 (I/O)의 세트

- 프로그램 f \in Y는 X_m과 관련된 문제를 풀 수 있는 함수로 다음을 만족

- 또한 $F_m$은 입력-출력 쌍을 생성할 수 있는 실제 함수를 나타냄
Program Synthesis Generalization
- 본 논문에서는 프로그램 $F_m$에 의해 생성된 입-출력 예시들과 함께 추가적인 입력 $x_{n+1}^m$이 주어짐

- 여기서 목표는 specification을 설명하는 것 뿐만 아니라 프로그램을 새로운 입력인 $x_{n+1}^m$에 적용했을 때도 성공적인 추론을 하는 것 → 일반화 성능!
- 이는 few-shot learning과 유사함
Variational Auto-Encoders (VAEs)
- Bayesian inference를 근사하는 프레임워크
- 목표는 데이터셋 $x$의 샘플이 주어졌을 때 posterior $p(z|x)$를 추론하는 것 → $z$: 잠재 변수 (latent variable)
- 직접적으로 posterior를 계산할수는 없으므로 이를 근사하기 위해 ELBO (Evidence Lower BOund)를 사용 → 해당 접근에서 실제 posterior 분포의 근사를 위해 파라미터화 된 인코더 $q_{\phi} (z|x)$를 사용
- ELBO는 다음과 같이 수식화 될 수 있음
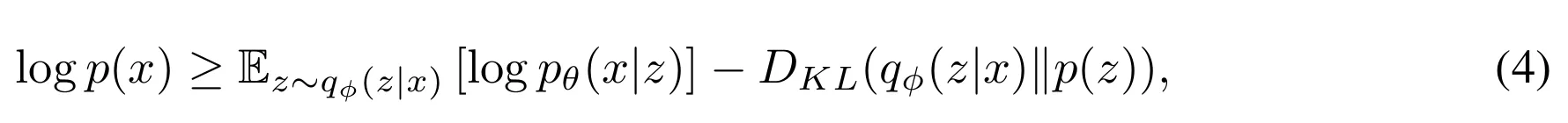
- 위 식에서 각 항의 역할에 대해 살펴보자
- 첫번째 항: 잠재 변수 $z$로부터 $x$를 재구성하는 확률을 나타냄
- 두번째 항: Kullback-Leibler divergence로 $q_{\phi} (z|x)$가 prior distribution $p(z)$에 가까워지도록 함
3. Latent Program Network
- 본 논문에서 제안하는 기법 → LPN (Latent Program Network)
- 입력-출력 쌍의 specification으로 인공신경망을 end-to-end로 학습하고 새로운 입력에 대한 출력을 생성
- 추상화, 탐색, 합성을 수행
- test-time adaptation을 수행하도록 디자인
- 3가지 주요한 요소로 구성되어 있음
- 인공신경망 인코더: specification $X_m$을 입력으로 하며 추상화 된 latent program을 출력
- 최적화 과정: 데이터를 가장 잘 설명하도록 latent를 정제
- 인공신경망 디코더: latent program을 실행하여 출력을 생성
- 기존 기법과 그 한계점
- 기존 기법은 주어진 specification에 대해 정확한 출력을 디코딩하는 확률을 최대화하는 모델을 직접적으로 학습하는 것에 집중
- 기존 기법의 한계점
- 다른 크기의 specification에 대해서 확장이 어려움
- 본 적 없는 문제로 일반화가 어려움
- 테스트 시점에 적응하는 능력이 없음
- 본 논문에서 제안하는 기법의 특징
- 시스템을 다음의 과정을 가지도록 명시적으로 나누어 설계
- (1) 추상화 생성 → (2) 잠재 프로그램 추론 → (3) 출력 예측
- 처음 보는 문제에 대해 test-time computation을 사용하여 적응할 수 있는 능력을 가짐
- 시스템을 다음의 과정을 가지도록 명시적으로 나누어 설계
3.1. Latent Program Inference
- 본 논문에서는 인코더와 디코더가 VAE와 유사한 역할을 수행하지만 잠재 벡터 최적화 (latent optimization)과정이 포함되어 동적인 최적화 문제를 해결하려고 시도함
- 또한 VAE와는 달리 테스트 시점에도 인코더를 잠재 프로그램의 시작점으로 사용 → 성능에 결정적인 요소
Encoder
- 확률적 인코더 (probabilistic encoder)는 Bayesian posterior를 근사하도록 학습 → 입출력쌍 $(x,y)$를 잠재 공간 $q_{\phi} (z|x,y)$로 맵핑
- Variational 접근이 중요!
- 어떤 주어진 입력-출력 쌍에 대해서도 입력에서 출력을 맵핑하는 프로그램이 존재할 가능성이 있음
- 이에 따라 인코더는 입력-출력 예시를 인코딩 하여 연속적인 잠재 공간에서 프로그램의 추상적인 표현을 배우도록 학습
- 본 논문의 구현에서는 인코더가 다변량 정규 분포 (multivariate normal distribution)을 사용
- 인코더가 평균 $\mu$와 대각 공분산 $\Sigma$을 추론
Decoder
- 확률적 디코더 (probabilistic decoder)는 잠재 프로그램과 입력을 출력의 공간으로 맵핑
- 출력은 바로 픽셀 기반으로 예측되며 DSL (도메인 특화 언어)를 사용해서 프로그램을 생성하는 방식은 아님
- 또한 해당 디코더는 입력 $x$와 잠재 벡터 (latent) $z$가 주어졌을 때 가능한 출력 $y$의 분포를 모델링
- 실제 프로그램이 결정적 (deterministic)이더라도 본 논문에서는 확률적 디코딩 프레임워크 $p_{\theta}(y|x,z)$를 사용 (maximum likelihood learning을 위해)
- 그림 2는 입력을 고정하고 잠재 프로그램을 변경했을 때 디코더가 생성하는 출력이 달라지는 것을 보임 → 디코더가 잠재 프로그램의 변경에 따라 다양한 출력을 도출할 수 있음을 확인

Latent Optimization
- 인코더는 프로그램에 대한 posterior를 근사하도록 학습하지만 입출력 쌍이 주어졌을 때 적절한 추상화를 인코딩하지 못할 수 있음
- 이 경우 잘못된 인코딩 결과가 디코더에 입력되므로 틀린 결과를 생성하게 됨
- 이에 따라 본 논문에서는 잠재 벡터 최적화 (latent optimization)라는 중간 단계를 도입
- 먼저 인코더의 예측 $z$에서 시작 → 디코더 $p_{\theta}$에 의해 관측된 데이터를 가장 잘 설명할 수 있는 더 나은 잠재 프로그램 $z'$를 탐색
- 해당 탐색 과정은 다음의 식과 같이 정의되며 다양한 방법으로 구현될 수 있음
- $z'=f(p_{\theta}, z, x, y)$
- 해당 구현 방법은 3.2에서 살펴볼 것!
- 결과적으로 인코더, 잠재 벡터 최적화, 디코더의 식은 다음과 같이 정리할 수 있음

3.2. Search Method for Latent Optimization
- $n$개의 입출력 쌍 $\{(x_i, y_i)\}{i=1,...,n}$이 주어졌을 때 탐색 과정 $z'=f(p{\theta}, z, x, y)$는 다음을 만족하는 $z'$를 찾는 것이 목적
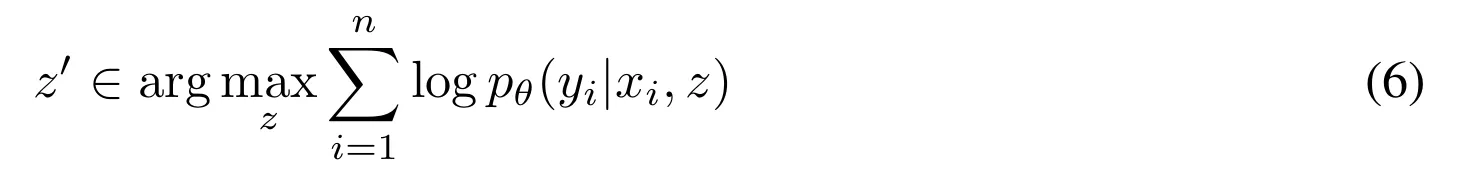
- 이는 입력이 주어졌을 때 디코더가 가장 올바른 출력을 생성할 것 같은 잠재 벡터 (latent)를 찾는 것
- 이를 위해 본 논문에서는 2가지 방법을 제안 → random search, gradient ascent
- 잠재 공간에서 더 나은 exploration-exploitation 트레이드 오프를 할 수 있는 새로운 exploration 방법은 future work!
Random Search
- Random search의 적용 방법
- prior 분포 $p(z)$나 근사된 Bayesian posterior $q_{\phi}(z|x_i, y_i)$ 근처에서 여러 잠재 벡터를 샘플링
- 그리고 그 중 디코더에 의해 입출력 쌍의 log likelihood가 가장 높게 도출될 것 같은 잠재 벡터를 선택

- Random Search의 장단점
- 점근적으로 실제 maximum likelihood 잠재 벡터 (식 6)으로 수렴할 수 있으며 최적화할 함수가 미분 불가능하거나 연속이 아닌 경우 유용
- 하지만 잠재 공간의 차원이 커질수록 효율성이 크게 떨어짐 → 많은 문제에 대해 실용적이지 못함
Gradient Ascent
- 디코더가 미분 가능한 인공신경망이므로 디코더의 log-likelihood $\log p_{\theta}(y|x,z)$ 또한 $z$에 대해 미분 가능
- 따라서 gradient ascent와 같은 방법을 사용하여 잠재 벡터 최적화 문제 (식 6)의 해답을 찾기 위해 잠재 공간에서 효율적인 탐색 가능
- 그림 3은 기울기 장 (gradient field)과 2D 잠재 공간의 디코더 log-likelihood를 나타내며 어떻게 gradient-ascent가 잠재 공간에서 지역 최적점을 찾는지 보임

- 위 그림 3을 살펴보면 다음과 같은 사항들을 파악할 수 있음
- 높은 디코딩 likelihood를 가지는 부분은 잠재 공간의 작은 영역 뿐
- 나쁜 초기화는 로컬 미니마 (local minima)로 수렴하도록 탐색을 수행함
- 해당 탐색에 대한 수식은 다음과 같음
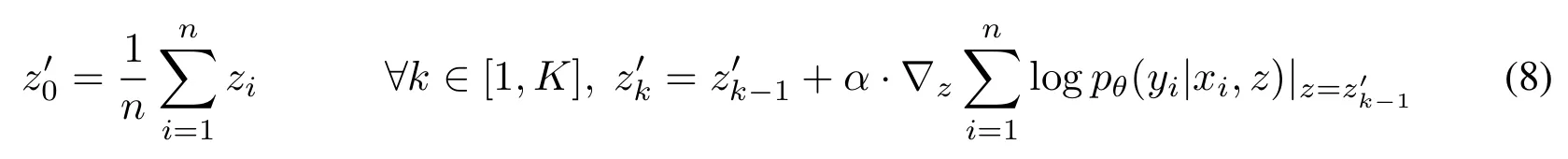
- $(z_k)_{k \in [1,K]}$는 스텝 크기 $\alpha$가 충분히 작으면 디코딩 likelihood가 증가해야함
- 또한 실제로 gradient ascent 알고리즘 동안 찾은 최고의 잠재 벡터는 항상 마지막 기울기 스텝 $(z_K)$에서 얻은 것은 아님
- Gradient Ascent 기법의 알고리즘은 Algorithm 1의 내용 참고
3.3. Training
- LPN 시스템을 end-to-end로 학습하기 위해서 각 문제 (task)가 동일한 프로그램으로 생성된 $n$개의 입출력쌍 $(x_i, y_i)$로 정의
- 테스트 조건을 반영한 학습 설계
- 주어진 specification으로부터 새로운 입력에 대해 예측을 수행하는 테스트 조건을 시뮬레이션하여 학습을 설계
- 이를 위해 학습 중 각 출력 $y_i$를 재구축하기 위해 해당 데이터 쌍 $(x_i, y_i)$을 사용하는 것이 아니라 나머지 $n-1$개의 쌍 $(x_j, y_j)_{j \neq i}$ 를 사용
- 이렇게 하지 많으면 인코더가 직접 출력 $y_i$를 압축하게 되어 프로그램과 관련된 추상화를 학습하지 못함
- 이제 출력 $y_i$의 재구축 과정을 살펴보자
- 모든 $j \neq i$에 대해 인코더 $q_{\phi} (z|x_j, y_j)$로부터 잠재 벡터 $z_j$를 샘플링
- 해당 벡터들의 평균을 계산 → $\frac{1}{n-1} \sum_{j \neq i} z_j$
- 다음으로 $z_i'$를 계산하기 위해 gradient ascent를 사용하여 잠재 벡터 최적화를 수행
- 그리고 입력 $x_i$와 정제된 잠재 벡터 $z_i'$을 사용하여 올바른 출력 $y_i$의 negative log likelihood를 계산
- 마지막으로 라벨 $y_i$와 디코더의 logit $p_{\theta} (\hat{y}_i| x_i, z_i')$의 크로스엔트로피 손실함수를 계산
- 위의 전체 학습 파이프라인은 알고리즘 2 참고

- 손실 함수 (loss function)은 2가지를 사용
- reconstruction loss $\mathcal{L}{rec}$와 KL loss $\mathcal{L}{KL}$

- 여기에 \beta라는 가중치 요소를 추가하여 reconstruction과 KL의 균형을 조절 → 최종 손실함수는 다음과 같음

- 재매개변수화 기법 (Reparameterization Trick)
- Reconstruction loss $\mathcal{L}_{rec}(\phi, \theta)$가 인코더의 파라미터 $\phi$에 의존하는 이유 → 각 잠재 변수 $z_j$를 샘플링 할 때 재매개변수화 기법을 사용하기 때문!
- 해당 기법은 다음과 같은 과정으로 수행
- 먼저 표준 정규분포에서 무작위 벡터를 샘플링 → $\epsilon_j \sim \mathcal{N}(0,I)$
- 인코더를 통해 평균 $\mu_j$와 대각공분산 $\Sigma_j$를 계산
- 이를 재구성하여 다음과 같이 최종 잠재 벡터를 계산
- $z_j = \mu_j + \epsilon_j \cdot \Sigma_j$
- 그리고 최종적으로 업데이트 된 잠재벡터 $z_i'$는 출력을 재구축하도록 디코더에서 사용됨
- 이때 디코더의 기울기가 latent update를 통해 전파되도록 결정할 수 있음
- 이때 업데이트 동안 기울기를 멈추는 것이 계산 효율적 → 알고리즘 2의 10번째 줄 참고
- 마지막으로 학습 과정에서 gradient ascent latent optimization을 사용하는 경우를 생각해보자
- 이 경우 계산량이 크게 증가
- 이에 따라 학습 시에는 0-5 스텝 정도로 작은 수의 gradient ascent 스텝을 수행
- 또한 mean training을 수행 → 0 gradient ascent 스텝을 수행하는 경우 잠재 벡터 최적화를 하지 않고 예측을 수행하기 위해 평균 잠재 벡터를 사용
4. ARC-AGI Experiments
- ARC-AGI 2024 챌린지를 테스트 도메인으로 사용
- ARC-AGI 2024 챌린지의 특징
- 다양하고 특색있는 문제로 구성된 program synthesis 데이터셋
- 아주 적은 학습 데이터셋 제공 (400개의 학습 문제로 구성)
- 벤치마크는 암기보다는 적응이나 OOD (out-of-distbitubion)에 대한 일반화를 요구함
4.1. LPN Architecture
- 프로그램은 ARC-AGI의 입력-출력 공간으로 정의
- 2D 그리드로 각 칸이 10개의 서로 다른 값을 가질 수 있으며 (n,m)의 크기를 가짐, $n,m \in [1,30]$
- 구현 사항
- 인코더와 디코더는 작은 트랜스포머 구조를 가지도록 구현
- 코드는 JAX로 구현했으며 인공신경망은 Flax 라이브러리를 사용
- 입출력 형식
- 입출력 이미지를 2D 모델링 후 pad, flatten을 수행하여 30*30=900의 크기를 가지는 픽셀값의 시퀀스로 나타냄 (그림 4 참고)
- 단, 각 그리드 시퀀스의 가장 앞에 열과 행의 수의 값 2개를 추가 → 총 902개의 값에 대한 시퀀스 사용
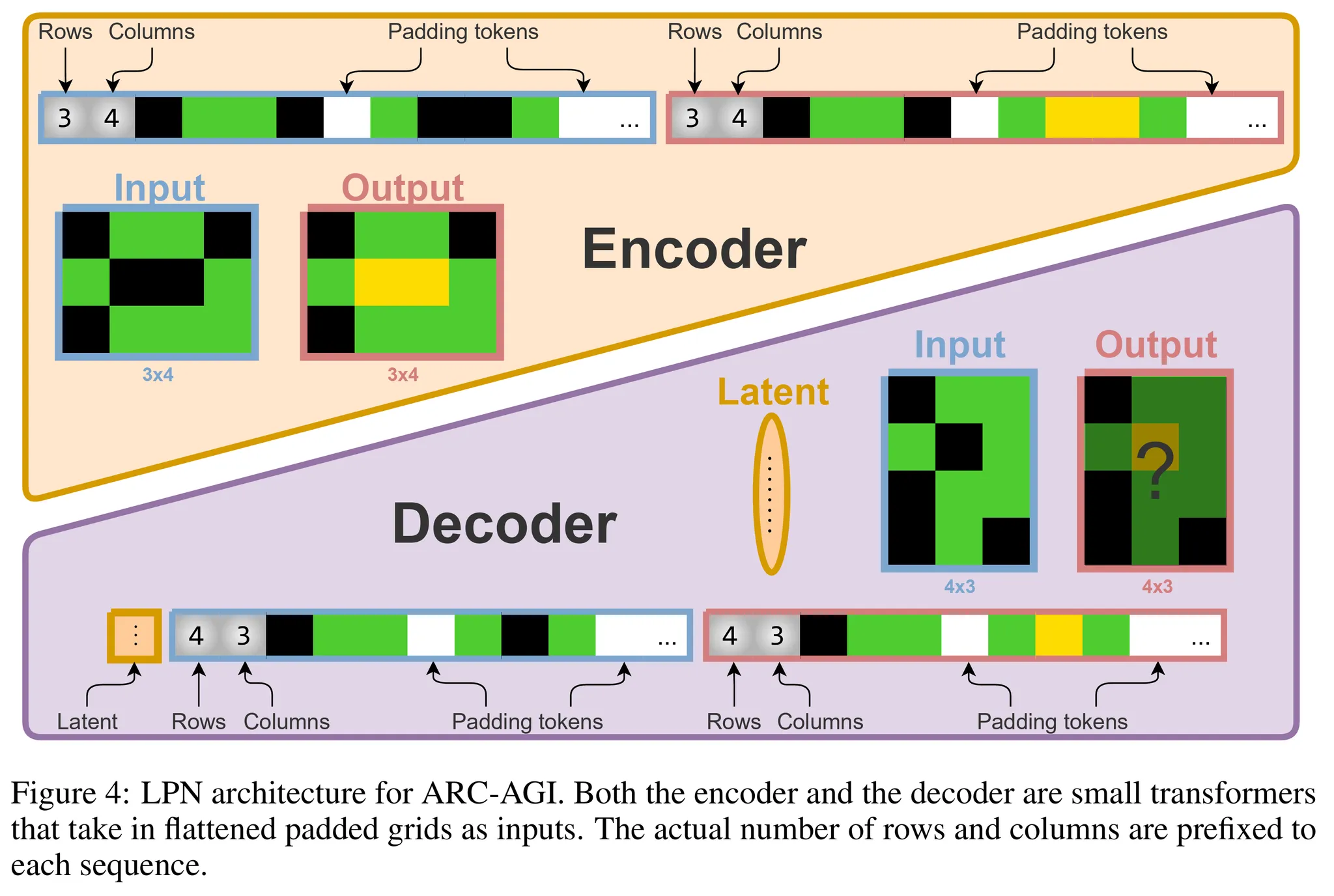
Encoder
- 추론 수행
- 입력과 출력 그리드를 모두 사용하여 주어진 문제에 대한 program letent의 추론 분포를 반환
- 구체적으로는 다변량 정규 분포 (multivariate normal distribution)의 평균과 대각공분산을 반환
- 각 그리드 데이터 구성
- 902개의 값으로 구성된 시퀀스 + 출력 임베딩을 위한 추가 CLS 토큰 사용
- 최종적인 인코더 트랜스포머의 총 시퀀스길이는 1805개 (입력 902 + CLS 토큰 1 + 출력 902)
- 공간적 정보를 위해 positional embedding 분해
- 다음과 같은 형태로 분해: $pe(i,j,c) = pr(i) + pc(j) + emb(c)$
- $i, j \in [1,30]$
- $c \in \{0,1\}$ → 채널 인덱스 (0=입력, 1=출력)
- $pr$: 열 (row)의 임베딩
- $pc$: 행 (column)의 임베딩
- 모든 임베딩은 $\mathbb{R}^H$에 포함 → $H$는 트랜스포머의 임베딩 사이즈
- 모든 1800개의 색에 대한 값은 0-9 사이의 값, 4개의 모양 (shape)에 대한 값은 1-30 사이의 값을 가짐
- 다음과 같은 형태로 분해: $pe(i,j,c) = pr(i) + pc(j) + emb(c)$
- 패딩 토큰은 마스킹하고 시퀀스를 다중 트랜스포머 블럭에 입력
- CLS 임베딩은 layer-norm과 2개의 병렬적인 dense layer를 통과하여 잠재 벡터에 대한 다변량 정규 분포의 평균과 대각 log 공분산을 출력
Decoder
- 디코더는 입력 그리드와 잠재 프로그램을 입력으로 하여 auto-regressive하게 출력 그리드를 생성
- 기본적으로 인코더와 유사하게 디자인 되었지만 몇가지 차이를 보임
- flatten 시퀀스의 가장 앞에 잠재 임베딩의 projection을 추가 (prefix)
- 디코더가 auto-regressive하게 출력을 생성하므로 시퀀스의 두번째 절반 (출력 그리드)에 대해 causal attention mask 적용
- 출력 시퀀스에 적용되는 attention mask는 예측된 출력의 크기에 따라 동적으로 패딩 토큰을 마스킹
- 출력에 해당하는 시퀀스의 임베딩만 추출 → 앞의 2개는 출력의 형태에 대한 logit으로 변환하고 나머지 900개는 그리드의 셀 값에 대한 logit으로 변환
- 출력 토큰은 일반적으로 가로로 스캔 (raster-scan)하는 방식으로 다음 토큰에 대한 logit을 맵핑하지만 각 줄의 패딩으로 인해 각 열의 마지막 임베딩은 다음 열의 첫번째 토큰으로 맵핑
4.2. Validating the Decoder
- 딥러닝 네트워크를 처음부터 학습시켜 ARC 같은 문제를 푸는 것은 어려움!!
- 만약 네트워크가 단일 프로그램에 대한 문제도 제대로 학습을 못하면 다양한 프로그램의 분포를 대상으로 학습하는 것은 불가능!!
⇒ 이에 따라 LPN을 end-to-end로 학습하기 전에 본 논문의 디코더가 단일 프로그램을 잘 학습할 수 있는지를 먼저 확인!
- 먼저 400개의 ARC-AGI 문제 중 5개를 선택한 다음 각 문제에 대해 800k의 크기를 가지는 작은 LNP 구조로 학습 (마지막 문제는 복잡해서 8.7M개 파라미터 사용)
- arc-agi_training_challenges.json 파일의 처음 5개 문제(007bbfb7, 00d62c1b, 017c7c7b, 025d127b, 045e512c)를 선택 (그림 5 참고)

- 학습된 모델을 아래의 2 조건에서 평가 (그림 6 참고)
- re-arc가 생성한 문제 분포 상에서의 성능
- ARC-AGI 원본 학습 데이터셋의 실제 문제에서의 성능

- 확인 결과 작은 LPN 디코더 모델이 성공적으로 개별 프로그램을 학습하고 ARC-AGI 과제의 문제를 해결할 수 있음을 보임!! 👍
4.3. Pattern Task
- ARC-AGI 챌린지는 서로 다른 사전지식을 요구하는 다양한 문제로 구성
- 이런 처음부터 ARC와 같은 데이터를 사용하여 사전지식을 LPN에 학습하는 것은 많은 양의 계산량을 요구
- 이에 따라 큰 규모의 학습 이전에 LPN의 학습 역학과 특성을 조사
- 이를 위해 단순한 문제인 패턴 문제 (Pattern task)를 사용 (그림 7 참고)
- 검은색의 10x10의 입력에 하나의 파란 픽셀이 랜덤하게 위치
- 해당 위치에 4x4 크기의 패턴을 추가

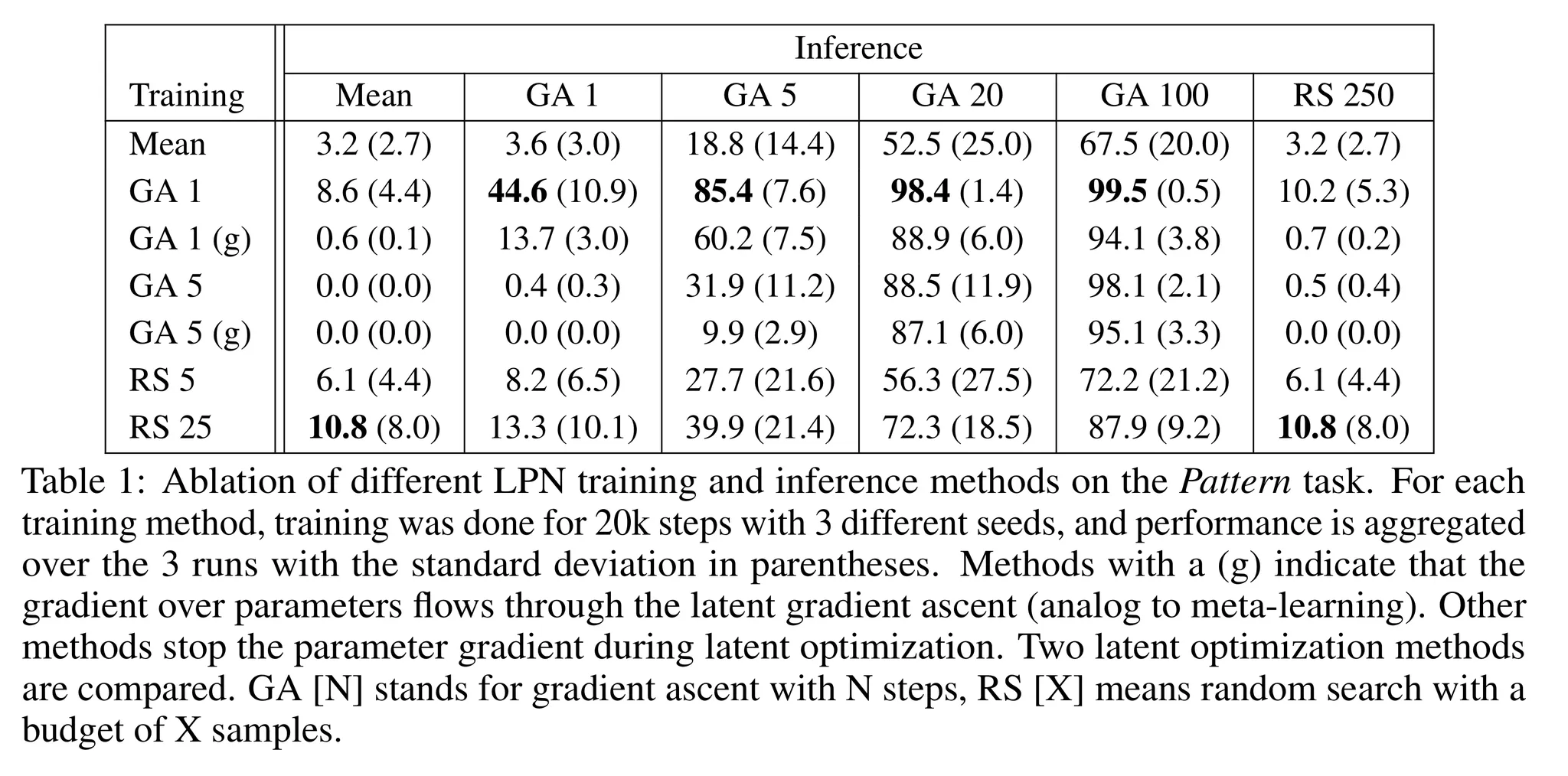
- 해당 문제에서 다양한 학습과 추론 비교한 결과 → 표 1 참고
- 1M 파라미터 모델을 128개의 배치 사이즈로 20k 학습
- 다른 시드로 3번 실험을 반복하여 평균 성능을 구했으며 표준편차를 괄호 안에 추가
- 결과 1
- Mean latent (잠재 벡터 최적화 수행 x)를 사용하는 경우 모든 학습 기법에 대해 좋지 못한 성능을 보임
- 정답 잠재 벡터를 한번에 추론하는 것은 어려우며 어떤 형태로든 잠재 프로그램 탐색이 필요하다는 것을 확인
- 결과 2
- 추론 시에는 잠재 벡터 최적화를 많이 수행할수록 정확도가 올라가는 것을 확인
- LPN이 많은 계산량을 사용할수록 테스트 시 새로운 문제에 더 잘 적응함을 보임
- 결과 3
- 1 스텝 gradient ascent의 잠재 벡터 최적화를 수행한 경우 mean latents를 사용했을 때보다 훨씬 높은 성능을 달성함을 보임
- Mean latent로 학습한 경우 100 스텝의 gradient ascent 추론을 했을 때 67.5%의 정확도를 달성했지만 1 gradient step으로 학습한 경우 99.5%의 정확도를 달성
- 결과 4
- gradient ascent 기법을 사용하는 것이 random search 보다 좋은 성능을 달성
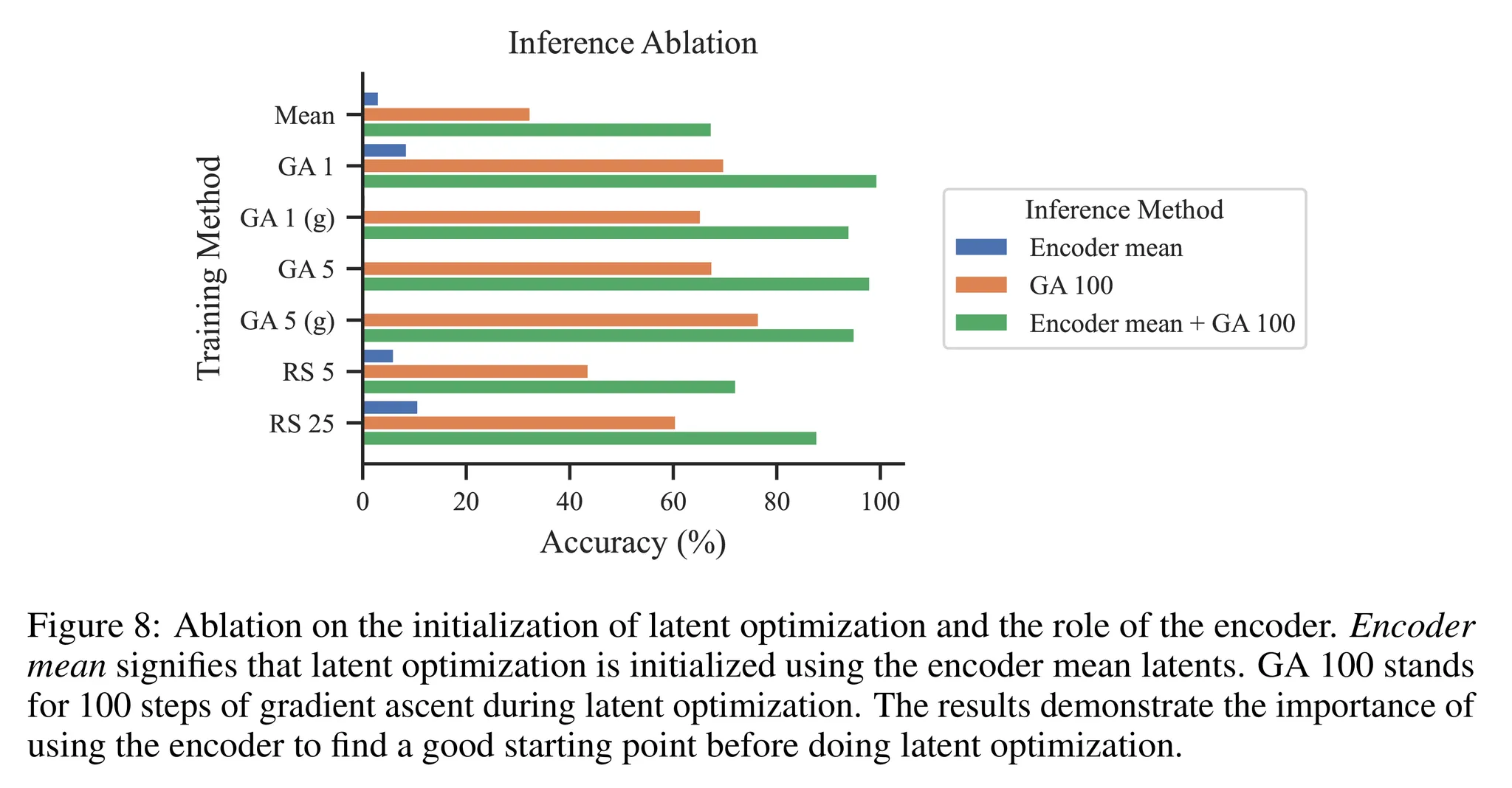
- 추가적으로 잠재 벡터 최적화시에 인코더와 prior로 초기화 했을 때의 결과를 비교
- 즉, $z \sim p(z)$와 $z \sim q_{\phi}(z|x,y)$의 결과 비교
- 그림 8을 보면 탐색을 위해 인코더를 사용하여 초기화하는 것이 모든 학습 기법에 대해 더 좋은 성능을 보임
4.3. Analyzing the Latent Space
- 인코더가 잠재 공간에서 프로그램을 학습한다는 것을 검증하기 위해 더 단순한 문제를 구성 → 2x2 크기의 패턴을 가지는 4x4 크기의 그리드
- 해당 문제에서 LPN을 수렴할 때까지 학습하고 2차원의 잠재 공간에서 시각화 → 그림 9

- 단순한 구현을 위해 Mean 방법으로 학습 수행
- 잠재 공간에 2D Gaussian prior를 사용 → 정규 누적 분포 함수 (CDF, Cumulative Distribution Function)를 사용하여 $\mathbb{R}^2$을 단위 정사각형 (unit square)으로 변환 후 단위 정사각형의 각 좌표 $(x,y)$를 디코더에 입력한 결과를 시각화 → $z=(CDF(x), CDF(y))$
- 이는 잠재 공간이 충분히 넓은 범위에 대한 인코딩이 가능함을 보임 → 특히 본적 없는 패턴에 적응하는데 중요한 요소!
4.5. Adapting Out-of-Distribution
- 서로 다른 학습 방법을 적용했을 때 OOD (Out-of-Distribution)에 대한 결과가 표 2에 정리되어 있음

- 패턴 문제를 사용하고 생성할 패턴을 서로 다른 색의 밀도 (density)를 사용
- 먼저 50%의 밀도로 학습을 수행
- 그리고 다음의 조건들로 평가를 진행
- 50%
- 75% (weakly OOD)
- 100% (strongly OOD)
- 결과를 살펴보면 gradient ascent를 사용하는 LPN이 OOD 세팅에서 강한 추론 성능을 보이는 것을 확인 (88% 정확도)
- 반면 mean latent를 사용한 경우 0%의 성능을 달성
4.6. ARC-API 2024
Data Generation
- 학습 단계에서 LPN 시스템에 핵심 사전 지식을 주입하도록 디자인
- re-arc generator를 사용하여 학습 동안 온라인으로 많은 입력-출력 쌍을 생성
Training
- LPN 모델은 39M 개의 파라미터를 가지며 256 차원의 잠재 벡터 공간을 가짐
- 학습 과정
- Mean training으로 학습 (학습 동안은 잠재 벡터 최적화 사용하지 않음)
- 220k의 학습 스텝 동안 TPU v3-8을 사용하여 128 배치로 5일 동안 학습 수행
- 이후 1스텝의 gradient ascent 잠재 벡터 최적화를 사용하여 2k 스텝만큼 모델 파인튜닝 수행
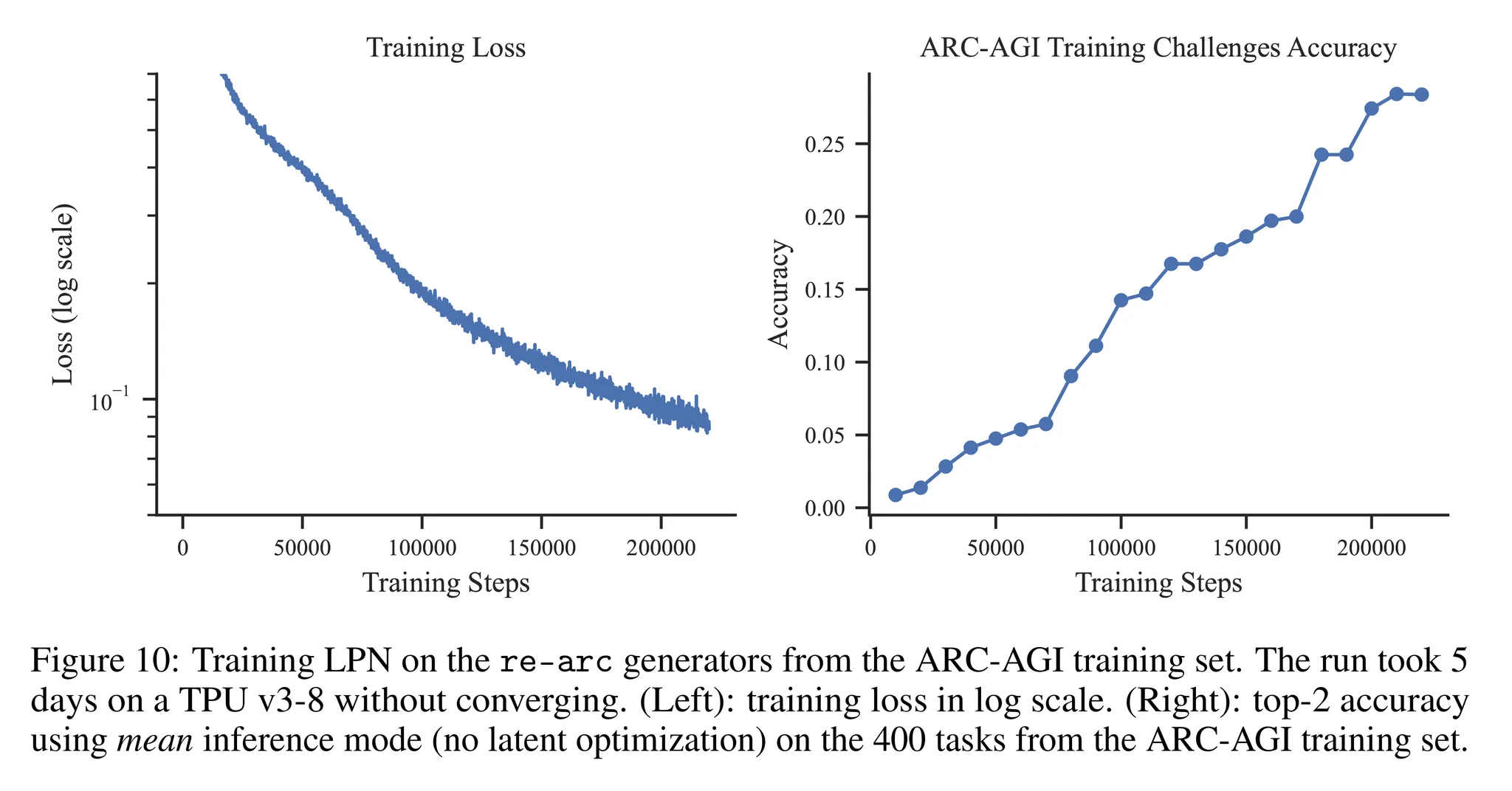
- 그림 10을 통해 학습 셋의 400개의 문제에 대해 모델의 top-2 정확도와 학습 손실함수를 살펴볼 수 있음 (mean latents를 사용하여 추론)
- 이때 아직 학습이 수렴하기 전 계산 비용의 한계로 인해 학습을 멈춘 것을 확인할 수 있음
Results
- 표 3을 통해 테스트 수행시 잠재 벡터 최적화를 확장한 결과를 살펴볼 수 있음

- Gradient Ascent 잠재 벡터 최적화를 위해서 Adam Optimizer 사용
- $\beta_1 = \beta_2 =0.9$로 설정
- 학습률은 초기에 1.0으로 설정한 후 cosine decay를 수행
- 해당 결과를 살펴보면 잠재 벡터 공간에서 gradient ascent의 스텝의 수가 증가함에 따라 성능도 함께 늘어나는 것을 알 수 있음
- 약 400 스텝 정도에서 성능이 수렴
- mean latent에 비해 300 gradient 스텝만큼 최적화를 수행했을 때 성능이 24.83% → 46.13%로 거의 두배가 되는 것을 확인
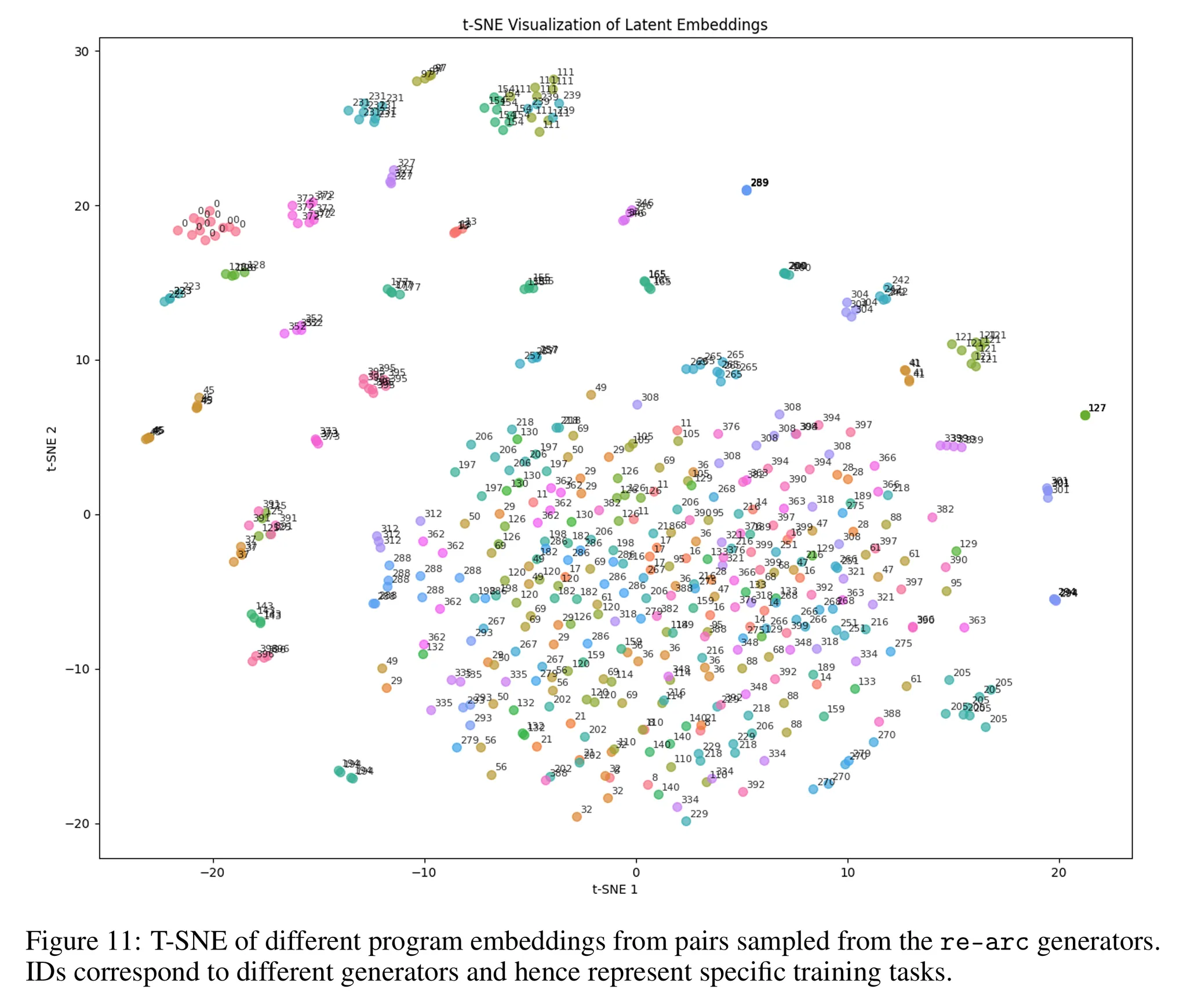
- 그림 11에서는 학습된 잠재 벡터 공간에서 T-SNE를 통한 시각화 결과를 살펴볼 수 있음
- 본 논문의 기법을 적용한 결과 검증셋 (evaluation set)에서 큰 일반화 성능을 보임
- 검증셋의 경우 학습셋 보다 문제가 더욱 복잡함
- 이 경우에도 gradient 스텝을 증가시킴에 따라 성능이 거의 3배가 증가하는 것을 확인 (Mean latent vs. GA 200)
- ARC 테스트 셋의 경우 정답을 알 수 없으므로 가장 검증셋의 성능이 높은 설정을 사용 → 3%의 정확도 달성
- 이를 통해 학습-검증셋보다 학습-테스트셋 사이의 일반화 차이가 더 크다는 것을 알 수 있음
- 하지만 그림 10에서 아직 학습이 수렴하지 않았다는 것을 확인한 만큼 더욱 높은 학습 정확도와 일반화 성능을 기대할만함
5. Conclusion
- 본 논문에서는 LPN (Latent Program Network) 기법을 제안
- 연속적인 잠재 벡터 공간에서 효율적인 탐색과 테스트 수행시 적응이 가능한 새로운 프로그램 합성 기법
- LPN은 직접적으로 구조에 테스트 수행시 적응 (test-time adaptation) 능력을 추가
- 잠재 벡터 공간에서 잠재 벡터를 정제하는 성능을 크게 향상시킴
- 또한 gradient 기반의 탐색을 사용하여 효율적인 적응이 가능하도록 함
- 이를 통해 LPN이 학습 분포를 넘어서 일반화되도록 함
- ARC-AGI 챌린지에서 성능을 검증
- LPN이 추가적인 합성 데이터 없이 학습셋을 넘어 검증셋까지 잘 일반화 됨을 확인
- 또한 LPN은 효율적으로 계산량을 증가시킬 수 있음 → 검증셋에 이어 테스트셋까지 더 높은 성능을 달성할 수 있음
- LPN 구조는 ARC-API 문제에서 기존의 비전 트랜스포머 기법들의 성능을 능가
- 기존 기법들의 경우 하나의 ARC 문제에 오버피팅 되는 문제가 있었지만 LPN은 180개가 넘는 arc 학습 셋의 프로그램이 실행 가능하도록 네트워크를 처음부터 학습
Limitations and Future Work
- LPN은 다음과 같은 한계점들을 가짐
- ARC-AGI 문제에서 수렴할때까지 충분히 학습되지 않음
- Future work: 이에 따라 연산량 증가 후 수렴시 특성을 분석
- Gradient ascent를 사용했을 때 local optima에 빠지는 문제!
- 이는 LPN이 최적의 잠재 벡터를 찾는 것을 제한
- Future work: 다른 최적화 기법을 적용하여 해당 한계를 해결
- 복잡하며 이산적인 (Discrete) 프로그램을 연속적인 잠재 벡터 공간으로 나타내는 것이 어려움
- Future work: 이산적인 프로그램의 표현 (representation)으로의 전환 가능 → 이산 공간 탐색이라는 어려움을 동반함
- ARC-AGI 문제에서 수렴할때까지 충분히 학습되지 않음
반응형